ВЗАИМОСВЯЗЬ ВЫХОДНЫХ И ОПРЕДЕЛЯЮЩИХ ПАРАМЕТРОВ СИСТЕМЫ

При анализе точности обработки на станках устанав­ливаются связи между случайными выходными парамет­рами Уі (погрешности обработки, уровни вибрации и др.) и’неслучайными переменными Х) (режимные факторы, нормы геометрической точности и жесткости, значения конструктивных параметров, уровни демпфирования сопряжений и стыков и др.). Такие связи исследуются регрессионными методами, поэтому необходимо привести основные положения и критерии, применяемые для оцен­ки достоверности результатов.

Основной предпосылкой применения регрессионного анализа является предположение о том, что для каждого фиксированного набора значений независимых перемен­ных хи Х2,…, хп случайная величина уц имеет нормаль­ное распределение с дисперсией, постоянной или пропор­циональной какой-либо заданной функции независимых переменных. Переменные леї, Х2, …, хп могут быть как случайными, так и неслучайными величинами и должны быть измерены с пренебрежимо малой ошибкой по срав­нению с ошибкой в определении значений у$.

Множественный регрессионный анализ предполагает два способа проведения экспериментального исследова­ния: пассивный эксперимент и активный. При пассивном сбор необходимого статистического материала осущест­вляется путем наблюдения за некоторым процессом или путем постановки эксперимента каким-то произвольным образом, основанным на интуиции или удобствах иссле­дования.

Активный способ предусматривает целенаправленное изменение факторов х{, по заранее спланированной схеме. Планирование [55] позволяет значительно снизить тру­доемкость экспериментального исследования. Однако при использовании активного эксперимента необхрдимо вме­шиваться в работу станка, стабилизировать требуемые конструктивные и технологические параметры или изме­нять их в широких пределах.

Важным этапом при построении математической мо­дели процесса обработки является выбор для нее формы связи, т. е. определение типа уравнений, выражающих количественные соотношения между показателями каче­ства и определяющими технологическими факторами. От правильного выбора зависит, насколько построенная модель будет адекватна изучаемому процессу.

Полученные эмпирические оценки точностных пара­метров аппроксимируются теоретическими зависимостя­ми, выражающими физическую сущность процессов, обу­словливающих изменение параметров. Если сущность физических процессов априори неизвестна, выбор теоре­тической зависимости производится таким образом, что­бы соответствие между эмпирическими и теоретическими данными было наилучшим. При этом в первую очередь следует использовать результаты теоретического анали­за погрешностей обработки. В ряде случаев существен­ную помощь в подборе формы связи могут оказать анализ и использование известных функциональных моделей, описывающих процессы обработки, аналогичные исследу­емым.

Так как теоретический анализ в общем случае не позволяет обосновать форму связи, то вид зависимости определяют на основании сравнения различных уравне­ний, отличающихся как по форме (линейные, нелиней­ные), так и по набору исходных факторов. Выбор наи­более адекватного уравнения может производиться статистическим путем с помощью коэффициента множест­венной корреляции R{y/xi) или множественного корреля­ционного отношения Г) (уІХі).

Понятию функции статистической связи между факто­рами Х{. и параметрами Уг соответствует уравнение по­верхности отклика. В общем случае функция связи (по­верхность отклика) записывается в следующем виде:

У* = /*(%, *а, хп). (1.16)

Так как аналитическое выражение функции (1.16) обыч­но неизвестно, приходится ограничиваться представле — нием ее полиномом

i=n п п п

Уг = ъ0+2 blXi+ 2 2 biiXiXi +2 ЬПХ’ (1Л?)

1=1 1=1 /= 1 t=l

где bt (і =1,2, …, л), %(і = 1, 2, …, /г, i=£j), bti—

коэффициенты регрессии соответственно при линейных чле­нах, взаимодействии факторов xt и ду и квадратичных чле­нах. Точность приближения к функции (1.16) может быть увеличена повышением степени многочлена (1.17).

При построении математических моделей процессов обработки с помощью методов планирования экспери­ментов используется «шаговый» метод [55] получения функции связи.

Поскольку практические задачи при исследовании металлорежущих станков заключаются в определении ин­терполяционных моделей или в достижении области оп­тимума, то, как правило, ограничиваются нелинейными уравнениями 1-го порядка. Коэффициенты уравнения (1.17) определяются методом наименьших квадратов.

В качестве критерия, характеризующего ошибку при описании экспериментальных данных математической мо­делью, может использоваться остаточная дисперсия S£t оценка которой определяется по выражению

N

{у и У и)2 ‘

———— Г’ (1Л8)

N— п — 1

где N, п — соответственно количество опытов и исследуе­мых факторов; уи — значения рассматриваемой погреш­ности обработки, найденные расчетным путем по модели.

Если экспериментальные данные хорошо аппроксими­

руются несколькими теоретическими зависимостями, вы­бирается та, для которой выполняется условие S^=min.

Гипотеза об адекватности представления результатов эксперимента полученной моделью проверяется с помо­щью Е-критерия Фишера. Если табличное значение Гтабл критерия Фишера при 5%-ном уровне значимости больше расчетного Fa, определяемого по формуле

Fa=S2R/Sz(y), (1.19)

то рассматриваемая модель считается адекватной.

Для количественной оценки тесноты статистической связи между факторами лу. и погрешностями уи в случае линейной формы моделей используется коэффициент мно-

У. Ь iy/Xi) г (y/Xi) S(Xi), (1.20) S(y) іТІ ГАеЬ(уІХг)—коэффициенты регрессии; r(y/Xi) коэф­фициент парной корреляции между у и х*; 5(хі) и S(y) среднеквадратические отклонения величин Хі и у соот­ветственно. Когда исходные факторы Хг взаимно некор — релированы, коэффициент множественной корреляции оп­ределяется по формуле І—П о-21) i= 1 Коэффициент R(y/xі) изменяется в интервале В случае функциональной связи jR=1. Если статистиче­ская связь между погрешностями обработки и рассмат­риваемыми факторами отсутствует, то R — 0. При практи­ческих расчетах, если R = 0,85—0,9, можно считать, что погрешности обработки адекватно описываются приня­той моделью. Значимость коэффицента множественной корреляции проверяется по ^-критерию Стьюдента: (1.22) * S(R) где S{R)—средняя квадратическая ошибка коэффициен­та множественной корреляции, определяемая по фор­муле 1 __ /Р2 0(р)—.,., . (1.23)

р

 

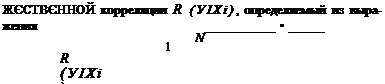где у—среднее значение рассматриваемой погрешности, полученное в процессе эксперимента. Значимость вычис­ленного значения г] (у/хи л;2,…, хп) устанавливается по ^-критерию Стьюдента с помощью зависимостей, анало­гичных формулам (1.23) и (1. 24).

При моделировании процессов обработки на станках с помощью методов математического планирования /

экспериментов (активный эксперимент) каждый опыт по матрице состоит из k параллельных. Результаты парал­лельных опытов обычно расходятся на некоторую вели­чину, характеризуемую дисперсией воспроизводимости, значения оценок S? (у) которой на различных уровнях должны быть однородны. Проверка однородности рядов S2f(y) производится [56] с помощью критериев Бартлет­та и Кочрена. Критерий Кочрена используется в случае одинакового количества экспериментальных данных в каждом параллельном опыте и определяется из выраже­ния

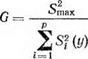(1.25)

где S^ax — максимальная расчетная оценка | дисперсии в опыте.

Полученное значение критерия G сравнивается с его критическим значением Gup, определяемым для 5%-ного уровня значимости по всем оценкам дисперсий Sf(t/), каждая из которых обладает п—1 степенями свободы.

Если G^Gkp, гипотеза однородности не отвергается,

Т. е. I

U

ІІ

%2 = _2^_[ngS2- 2f, lgS?(y)]2; (1.26)

ь Z=1

где значения С и S2 определяются из формул:

(1.27)

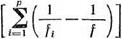
S2 = — l-2(^-1)Sf(l/)- (1 -28)

П —p i±i

Здесь f — число степеней свободы; ft — число степеней свободы в отдельной выборке; р—количество выборок;

Г= (1-29)

1=1

Расчетное значение X2 сравнивается с критическим 5%-НЫМ уровнем X2 , при f = p— 1 степенях свободы. При выполнении условия X2 <1X2 j гипотеза однород­ности дисперсий не отвергается. В противном случае дис­персии неоднородны.

В случае подтверждения гипотезы об однородности значений S? (у) на различных уровнях дисперсия S2 (у) (ошибка эксперимента) определяется по формуле

N К

2 2 (Урч f?)2

Здесь К — число повторных опытов на одном уровне; N — число опытов по матрице планирования экспери­мента.

Если число повторных опытов k на отдельных строках матрицы неодинаково, то величина Sz(y) определяется как среднее значение дисперсий Szt (у) по выражению

„2/ Ч ^ (у) fol + ^2 {у) &2 + — • • —S% (у) bN (1 .31)

(У) — Ьі + К + • • • + bN

где Ь>1 = Ъ (y/Xi) — коэффициенты регрессии.

Адекватность полученной модели проверяется с по­мощью F-критерия Фишера, определяемого по формуле (Г-19).

Все коэффициенты регрессии Ьг при планировании эксперимента оцениваются независимо друг от друга.

Доверительные границы для каждого из них вычисляют­ся по формуле

(1.32)

где 1К — табличное значение 1-критерия Стьюдента при числе степеней свободы Ъ, с которым определяется зна­чение S2(y).

Оценка значимости коэффициентов bi (проверка нуль — гипотезы |Зг-=0) производится с помощью 1-критерия по формуле

1, = bt ~VN/S (у). (1.33)

Полученные значения 1г — сопоставляются с их табличными значениями при том числе степеней свободы, с которым была определена ошибка эксперимента S2(y). Если ка­кой-либо из коэффициентов bi или Ьц оказывается не­значимым при 5%-ном уровне значимости, то его отбра­сывают, не пересчитывая все остальные.