РАСПРЕДЕЛЕНИЕ ПОГРЕШНОСТЕЙ ОБРАБОТКИ И ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МГНОВЕННОГО РАСПРЕДЕЛЕНИЯ

Статистические показатели точности обработки, опре­деленные по данным мгновенных распределений погреш­ностей, характеризуют точностное состояние собственно станка в период ti его эксплуатации в определенных усло­виях. Мгновенное распределение размерных погрешно­стей обработки, как правило, подчиняется нормальному закону, который имеет место тогда, когда на ход техно­логического процесса влияет множество случайных фак­торов при отсутствии доминирующих [7]. Однако, как показывают исследования [8, 12], при обработке деталей действует ряд процессов, смещающих уровень настройки станка во времени и приводящих к изменению зоны рас­сеивания погрешностей обработки. В результате суммар­ные распределения погрешностей, как правило, отлича­ются от нормальных.

Плотность распределения суммарных погрешностей обработки при наличии смещения центра мгновенного распределения погрешностей, характеризуемого функци­ей y(t) и изменением характеристик самого мгновенного распределения в соответствии с функцией b(t), может быть представлена выражением

х—а<,+уУ)У

где /0, tr — рассматриваемый интервал времени; а()—значе­ние функции у (t) в момент времени t0.

Наличие закономерно изменяющихся погрешностей (износ режущего инструмента, температурные деформа­ции системы СПИД, погрешности настройки, вносимые оператором, и т. д.) влияет на форму кривых распреде­лений; при больших значениях этих погрешностей рас­пределения могут сильно отличаться от нормального.

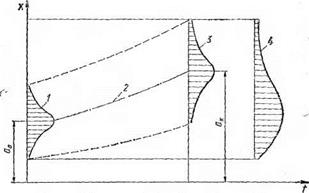
Рис 1.3. Схема образования суммарного распределения при смеще­нии центра группирования во времени и переменном рассеивании: I — q>(x, to); 2 — а(1); .3 — ф(х, t„); 4 — tp£ (аг)

Результаты исследований кривых распределения по­грешностей механической обработки различных операций (токарных, фрезерных, сверлильных и т. д.) [4, 9—11] подтверждают, что во многих случаях эти распределения не подчиняются нормальному закону (рис. 1.3). Наибо­лее существенное влияние на закон распределения по­грешностей механической обработки оказывает измене­ние уровня настройки и размера деталей при работе по методу пробных проходов, когда размер детали является функцией размера, определенного при пробном промере.

Отсутствие среди частных погрешностей резко доми­нирующих над остальными (по своему влиянию на об­щую погрешность) может быть обеспечено при обработке деталей на станках-автоматах, а также неавтоматизиро­ванных станках обычных типов (токарные, фрезерные, шлифовальные, револьверные и др.), настроенных на ра­боту по упорам, т. е. с одной настройки для всей партии обрабатываемых изделий. Кроме того, необходимо, если речь идет о деталях одной партии, чтобы при их обра­ботке не было сильного износа и затупления инструмен­та, резкого изменения температурного режима, система­тического изменения усилий резания, смены инструмента или поднастроек, смещающих центр группирования от­клонений размера, подачи другой партии заготовок с другими припусками или с другими механическими свой­ствами.

При классификации факторов, обусловливающих не­соответствие закона распределения погрешностей обра­ботки ф(Х) нормальному, можно выделить следующие причины: добавочные деформации узлов станочной си­стемы из-за колебаний усилий резания в зависимости от изменения режимов обработки, затупление режущего ин­струмента, износ и старение систем станка. Поэтому весьма существенно выделить из суммарного распреде­ления погрешностей обработки составляющую, которая характеризует их мгновенное распределение и мгновен­ную точность обработки.

Ошибку при определении характеристик рассеивания мгновенного распределения, возникающую в результате изменения центра группирования погрешностей обработ­ки, а также изменение величины самого рассеивания стремятся уменьшить за счет сокращения объема выбор­ки, что, однако, неизбежно приводит к снижению досто­верности результатов. Как показывают эксперименталь­ные исследования погрешностей деталей, обработанных на токарных, плоско — и бесцентровошлифовальных и дру­гих станках, параметры мгновенного распределения наи­более точно определяются при выделении закономерно изменяющихся слагаемых суммарного распределения. При этом погрешности обработки x,(t) последовательно обработанных деталей целесообразно рассматривать в виде суммы составляющих:

X; (I) Л’т (t) + У (/), (1.3)

где л’т(t) —составляющая, определяемая точностным со­стоянием станка; y(t)—составляющая, определяемая величиной смещения во времени центра группирования. погрешности обработки.

Выбор метода определения параметров мгновенного распределения погрешностей производится в зависимое-

ти от условий обработки на станке. При одновременной обработке партии деталей, когда этот процесс прекраща­ется одновременно на одном уровне настройки (обработ­ка партии деталей на плоскошлифовальных станках с круглым столом), параметры мгновенного распределения вычисляются по результатам измерения деталей одной партии или как среднее нескольких партий (в случае од­нородности характеристик рассеивания). Оценка средне­

квадратического отклонения параметров партии деталей находится по выражению

і / 2(*г-*)[1] [2]

s= у 1=__х ■ (1-4)

где Х{ — значение погрешности контролируемого пара­метра і-й детали; х — оценка математического ожидания погрешностей соответствующего параметра обработки.

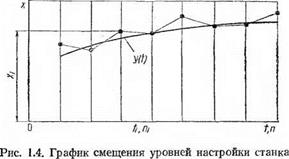
В случае последовательной обработки деталей или групп деталей на предварительно настроенном станке при наличии монотонного изменения уровня настройки, например из-за износа режущего инструмента (рис. 1.4), оценка среднеквадратического отклонения мгновенного распределения может быть определена из уравнения
где Уі(0 —значение функции y(t) уровня смещения на­стройки при обработке t-й детали.

Функция смещения уровня настройки y(t) находится путем сопоставления эмпирических зависимостей значе­ний контролируемого признака Хг от порядкового номера детали п (времени работы станка /) с известными функ­циональными зависимостями.

Уравнение (1.5) дает более точный результат в том случае, если искомое значение S практически постоянно на исследуемом интервале. В противном случае опреде­ляется усредненное на интервале М значение данного по­казателя.

Исходя из того, что первое слагаемое уравнения (1.3) представляет собой некоррелированную, а второе — кор­релированную составляющую отклонений размеров по­следовательно обработанных деталей, в работе [5] при­веден метод определения оценки среднеквадратического отклонения мгновенного распределения с помощью спект­ральной плотности. При этом отмечается, что для про­цессов со стационарным случайным смещением уровня настройки или близким к нему, типичным для обработки на станках с приборами активного контроля, этот метод дает более точный результат.

Последовательность размерных отклонений деталей, об­работанных без подналадок, рассматривается как реализа­ция Xj (.t) случайного процесса х (t) изменения погрешностей обработки на станке. В этом случае аргументом t процес­са являются номера обрабатываемых деталей. При каждом значении t (t — 1,2, . .., п) реализация xj (t) представляет собой значение хп случайной погрешности x(t) рассматри­ваемого точностного параметра в данном цикле обработки. Совокупность из т отдельных последовательностей погреш­ностей деталей представляется как множество реализаций Xj (і), (/= l, m). Оценки mx(t) и (t) для математического ожидания M{x(t)} и дисперсии D {х (/)} процесса х (t) в /-й реализации вычисляются по формулам

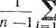(1.6)

(1.7)

2. Зак. 1257

Исходный процесс x(t) в этом случае анализируется в виде суммы двух составляющих, аналогичных выраже­нию (1.3).

Разделение суммарной погрешности и определение параметров ее составляющих производятся с помощью оценки спектральной плотности 5*;(со). Для этого процесс x(t) аппроксимируется теоретической функцией по ме­тоду наименьших квадратов, в результате выделяется составляющая, обусловленная систематическими факто­рами. Затем в каждом цикле обработки вычисляются отклонения от систематической составляющей. Центриро­вание процесса удовлетворяет одному из условий стацио­нарности, поскольку в этом случае значения x(t) на всем его протяжении тождественно равны нулю. Два других условия стационарности процесса x(t) заключаются в следующем: дисперсия S2(t) погрешностей сохраняется постоянной во времени (S2 (7) = const) и корреляционная функция Kx(ti, U) зависит только от величины промежут­ка Т = tk—ti времени, для которого она вычисляется, и не зависит от выбранного начала отсчета времени, т. е.

KAU, ^)=КДт). (1.8)

Оценка функции Кх (th tk) центрированного процесса x°(t) может быть определена из выражения

Kx(ti, Д)=—— — 2 lx(fi)~mx(ti)][x(th)—mx(tk)], (1.9)

п— 1 г=1

где тх (t) и тх (tk) — оценки математических ожиданий погрешностей соответственно в t-м и k-u циклах обработки, рассчитанные по множеству реализаций х (і).

Оценка Sx (<о) спектральной плотности вычисляется че­рез известные значения функции Кх(т) по формуле

= -^М2 2Kx(r)coson + Kx(0)i (1-Ю)

2л 1 гт“і J

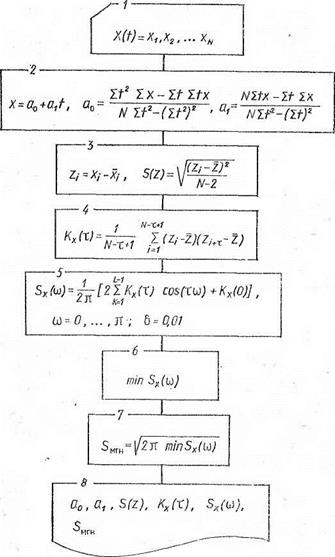
Анализ отдельных составляющих в исходном процессе (/) производится на основании графика функции Sx (со). Если для спектральной плотности стационарной случайной последовательности имеется хотя бы одно значение сої в интервале [—л, л], для которого ДДод) = 0, то это сви­детельствует об отсутствии в данной последовательности

Рис, 1.5. Блок-схема программы расчета составляющих суммарной погрешности обработки

мгновенной составляющей, так как при ее наличии спра­ведливо неравенство Sx (to) > 0.

Когда в исходной последовательности х° (t) имеется мгновенная составляющая — у (/), минимальное значение Sx (to) систематической составляющей х (t) также равно ну­лю, а минимальное значение (to) в этом случае совпада­ет с величиной Sy. Исходя из этого, значение Sv можно определить как наименьшее в интервале [—л, л] значение Sx(cо) спектральной плотности процесса х° (I):

Sy = minS,,. (to). (1.11)

Оценка дисперсии мгновенной составляющей погреш­ности обработки может быть рассчитана [12] по формуле

S* , гяттЯ^со). ‘ (1,12)

Алгоритм расчета составляющих суммарной погреш­ности обработки приведен на рис. 1.5. На основании дан­ного алгоритма составлена программа расчета на ЭВМ ЕС-1035. Использование ЭВМ позволяет значительно со­кратить трудоемкость работ при выявлении источников и анализе причин образования погрешностей обработки на металлорежущих станках.

В качестве примера распределения погрешностей об­рабатываемых деталей представлены фактические дан­ные, полученные при исследовании операций шлифования методом врезания на круглошлифовальнйіх бесцентро­вых станках мод. ВШ 531 Витебского завода им. С. М. Кирова и аналогичных станках мод. Р150С (Италия)..

Законы распределения размерных отклонений деталей, обработанных за межналадочный период на указанных станках, не соответствуют нормальному закону, что обу­словлено смещением уровней настройки за этот период вследствие износа шлифовальных кругов.

На рис. 1,6 представлена реализация центрированного случайного процесса изменения размерных отклонений деталей (обработанных на круглошлифовальном бес­центровом станке мод. ВШ 531) после исключения систе­матической составляющей, а также соответствующие графики корреляционных функций и спектральной плот­ности рассматриваемых случайных последовательностей. Графики корреляционных функций /Сж(т), рассчитанных для различных участков процесса Хо(п) с шагом т=1, оказались практически совпадающими. График спект-

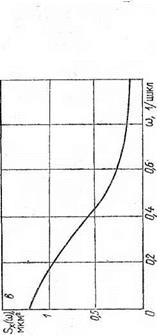
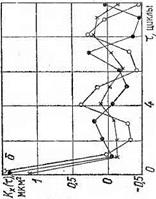
ральной плотности Sx(oj) имеет ярко выраженный мини­мум, что свидетельствует об отсутствии у процесса Х°(п) систематической составляющей.

Таким образом, процессы изменения размерных от­клонений деталей, изготовленных за межналадочный период после приработки шлифовальных кругов, можно рассматривать как стационарные случайные процессы, наложенные на неслучайные линейные функции от номе-

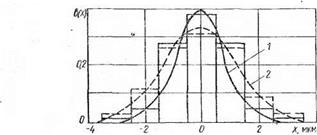
Рис. 1.7. Гистограмма частот и кривая плотности мгновенных рас­пределений диаметральных отклонений деталей: 1 —станки мод. ВШ 531; 2 — мод. PI50C

ра цикла обработки. После центрирования, т. е. исклю­чения в каждом цикле обработки уровня настройки, их параметры можно определять не по множеству реализа­ций, а по одной реализации достаточной протяженности, а также использовать корреляционно-спектральные мето­ды разделения погрешностей деталей на отдельные со­ставляющие.

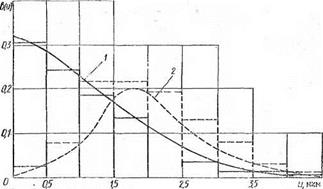
На рис. 1.7 приведены гистограммы частот и кривые плотностей мгновенных распределений размерных откло­нений деталей. Проверка по критерию Пирсона %2 под­тверждает соответствие их распределений нормальному закону. В то же время распределение погрешности фор­мы этих же деталей (овальности) подчиняется (рис. 1.8) законам распределения существенно положительных ве­личин, в данном случае закону модуля разностей, кото­рый необходимо использовать для определения средней величины погрешности формы при расчете суммарной зоны рассеивания погрешностей.

При обработке выборочной партии с переустановкой инструмента или заготовки с помощью настроечных ор­ганов станка после обработки каждой детали или груп­пы деталей мгновенное распределение погрешностей,

обусловленное процессом обработки, суммируется с рас­пределением погрешностей настройки, В этом случае значение параметра S мгновенного распределения по­грешностей обработки после выделения систематической составляющей находится по выражению

S = VS» — S* — rXBSESx, (1.13)

где Sx — оценка среднеквадратического отклонения сум­марного распределения; SH— оценка среднего квадрати­ческого отклонения распределения уровней настройки; гхи — коэффициент корреляции, определяющий тесноту статистической связи между погрешностями обработки и уровнями настройки. При независимости погрешностей обработки от уровня настройки гхн=0.

Приведенные статистические оценки позволяют оце­нить точность обработки по данным измерений точностных параметров деталей или по результатам оценки рабочих характеристик отдельных систем станков (настроечных органов, систем позиционирования и т. д.). Эти методы предполагают наличие станка, на котором может произ­водиться обработка или параметры которого могут быть измерены с требуемой точностью.

Методы оценки точности функционирования на ста­диях создания оборудования могут быть сведены [10, 13, 15] к изучению погрешностей перемещений замыкающих звеньев размерных и кинематических цепей систем

Рис. 1.8. Гистограммы частот и кривая плотности распределений погрешностей формы деталей: 1 — станки мод. ВШ 531; 2 — мод. Р 150 С

СПИД. Причины появления погрешностей обработки поэтому необходимо искать, рассматривая в целом стати­ческое и динамическое состояние системы. Как отмеча­лось выше, существующие методы расчета погрешностей обработки позволяют получать математические соотно­шения, связывающие погрешности формы обрабатывае­мых поверхностей деталей с геометрическими параметра-‘ ми расположения или относительного перемещения исполнительных органов станка. Эти методы не позво­ляют определить параметры распределений размерных погрешностей или погрешностей формы обрабатываемых деталей.

Для определения вероятностных характеристик точ­ности функционирования исполнительных органов станка исходят из того, что динамические свойства системы СПИД определяются такими их конструктивными пара­метрами, как величины и взаимное расположение масс отдельных деталей и систем, жесткость деталей и стыков, коэффициенты трения, величины зазоров в сопряжениях и т. д. Качество динамической системы определяется тем, насколько выбранное конструктивное решение обеспечи­вает уменьшение погрешностей перемещений формообра­зующих систем станка, обусловленных различными воз­мущающими воздействиями.

Динамическая система станка рассматривается как замкнутая, в зоне резания которой возбуждается нагруз­ка F(t), представляющая случайный процесс, который обусловлен многими факторами, такими, как непостоян­ство скоростей перемещения исполнительных органов, неравномерность припуска под обработку, неоднород­ность механических свойств обрабатываемого материала и т. д. Случайный процесс F(t) обусловливает относи­тельные колебания исполнительных органов системы СПИД, которые в свою очередь также могут быть пред­ставлены в виде процесса g(t). Как показывает анализ эксплуатационных данных, большинство возмущающих воздействий, обусловленных процессами функционирова­ния системы станка в установившемся режиме, носит стационарный характер. Уравнения движения относи­тельных масс и формообразующих систем станка могут быть представлены в общем виде:

П П

Mkgk + 2 hfn gt + 2 Chi~ Fh ‘ m< (1-14)

i=l 1=1

где Ми — обобщенные массы подвижных элементов стан­ка; км, — коэффициенты, связанные соответственно с коэффициентами демпфирования и жесткости; gu — обобщенные координаты относительных перемещений масс подвижных элементов станка; Fk(t) —обобщенные силы, связанные со случайной нагрузкой F(t). Причем следует учитывать, что при прогнозировании точности обработки оцениваются относительные колебания режу­щего инструмента и обрабатываемой детали в зоне реза­ния, обусловливающие закономерности образования по­грешностей.

В связи с тем что параметр g(t) в выражении (1.14) представляет собой случайный процесс с математическим ожиданием Mg=Q и дисперсией сг|, среднеквадратическое отклонение og, характеризующее точность функциониро­вания системы, может быть определено из выражения

/

-Г°°

| Ф (/to)|2SF (m) da, (1.15)

і’де Ф(т) —передаточная функция станочной системы; Si? (со)—спектральная плотность возмущающего воздей­ствия (процесса F(t)).

Показатели точности функционирования систем могут быть определены путем решения уравнений (1.14) по дан­ным конструктивных параметров, взятых из чертежа. При этом система станка должна быть детализирована на­столько, чтобы в уравнение вошли все основные конст­руктивные параметры, определяющие его работоспособ­ность. В этом случае коэффициенты жесткости и демпфи­рования приобретают реальный физический смысл, и значения этих коэффициентов можно рассчитывать по имеющимся в литературе данным для основных видов сопряжений. Представление же динамической системы станка в виде двух-, трехмассовой модели дает большое расхождение между расчетными и фактическими резуль­татами, вследствие того что многие узлы и подсистемы, оказывающие существенное влияние на передаточные свойства станка, не учитываются. Обобщение же их коэф­фициентов жесткости и демпфирования ведет к физиче­ской неопределенности и недостоверности получаемых ре­зультатов. В качестве исходных для расчета величины SF(ох) на проектной стадии могут быть использованы эк­
спериментальные данные, полученные по результатам исследования станков-аналогов. Расчет ag по выраже­нию (1.15) позволяет выбрать наиболее оптимальный вариант конструкции на проектной стадии.