Исследование 3D напряженно-деформированного состоя­ния (НДС) зоны шлифования

Если материал сохраняет свойство линейной упругости вплоть до раз­рушения, например, алмаз, за исключением небольшой окрестности верши­ны трещины, то учет влияния трещины нормального отрыва на прочность тела может быть осуществлен с позиций линейной механики разрушения. Однако, определение параметров разрушения представляет собой сложную физическую и математическую задачу, аналитические решения которой по­лучены только для частных случаев. Для решения задач со сложной геомет­рией и условиями нагружения обычно применяют численные методы, среди которых наибольшее распространение получил метод конечных элементов (МКЭ).

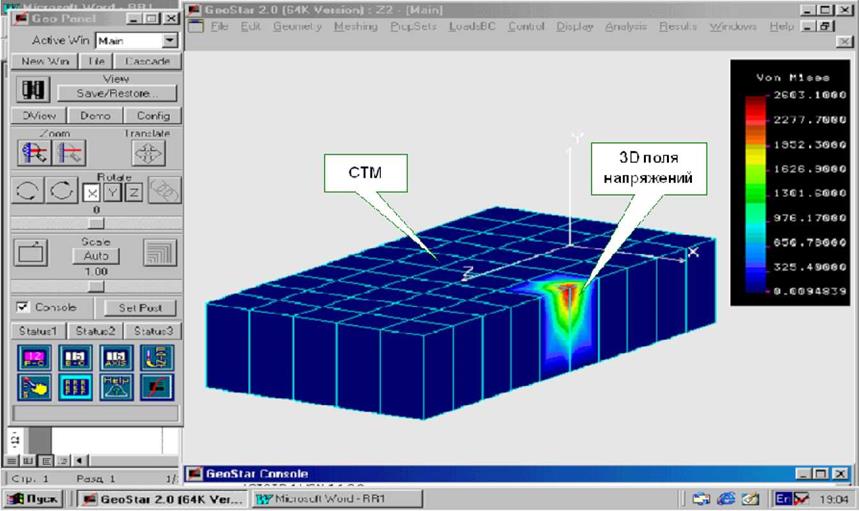
В настоящее время разработаны и эффективно используются целый ряд пакетов программ по методу конечных элементов, которые обладают большими возможностями. Из зарубежных наиболее распространенными яв­ляются пакеты типа «Cosmos», «Ansys» и «Nostran». В данной работе были использованы пакеты, аналогичные типам «Cosmos» и «Ansys». Пакет по­зволяет в трехмерном измерении (3D модель) рассчитывать поля приведен­ных и главных напряжений, энергию и плотность энергии деформации, тем­пературные поля и поля термосиловых напряжений, а также частоту собст­венных колебаний алмазных зерен. Окно программы представлено на рис. 2.7. Пример расчетов приведенных напряжений в элементах 3D системы «СТМ-зерно-связка» приведен на рис. 2.8 и в приложении А. На шкалах ре­зультатов расчета условно обозначены: Von Mises — приведенные напряже­ния, МПа; ENERGY — энергия деформации, SED — плотность энергии де­формации; ESTRN — деформация; Princ_1(2,3) — главные напряжения.

Важным достоинством метода является возможность одновременного изучения напряженно-деформированного состояния (НДС) во всех элемен­тах единой 3D системы «СТМ-зерно-связка» с учетом их взаимовлияния при различных физико-механических свойствах элементов системы и усло­виях ее нагружения. Вклад каждого из рассмотренных факторов в общий съем шлифуемого СТМ и другие выходные показатели определяются тем, как функционирует вся система «СТМ-зерно-связка». Дифференцирован­ный подход, применявшийся другими исследователями [115, 160], к изуче­нию явлений, протекающих в зоне шлифования, нивелирует выявление роли взаимовлияния элементов, в частности связки, влияния ее свойств на напря­жения в контакте «СТМ-зерно».

При исследовании взаимодействия зерна с поликристаллом рассматри­ваются модели, в которых связка, зерно и поликристалл полагаются упруги­ми сплошными телами. Поскольку наиболее распространенной формой кри­сталлитов (монокристаллов) алмаза считается октаэдр, форму 3D конечных элементов в МКЭ принимали близкой к нему. Такой подход обоснован еще и тем, что при разрушении алмаза продукты разрушения (частицы) имеют именно форму октаэдра [62].

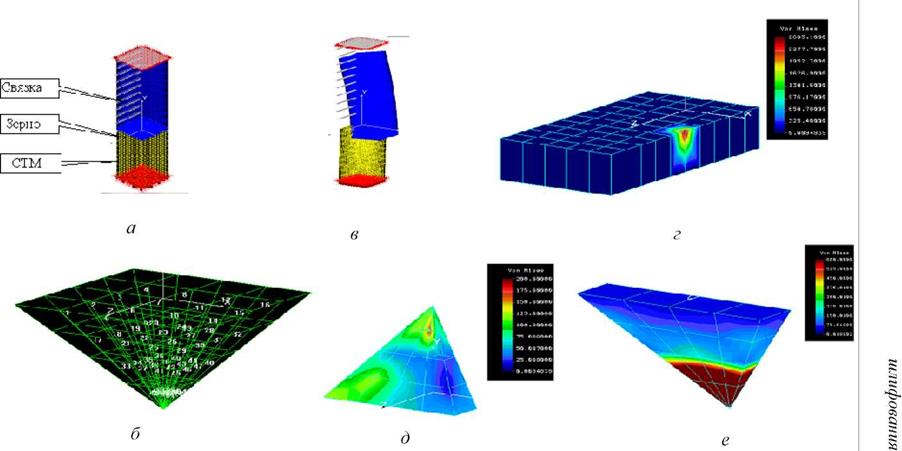
Связка и поликристалл при моделировании представлялись в виде призматических фрагментов с размерами соответственно 1x1x3 мм и 1x1x2 мм, а зерно — в виде октаэдра с размерами 200x140x140 мкм, что по­зволяет достаточно точно моделировать деформирование фрагментов моде­ли с учетом удаленности зон краевых эффектов. Расчетная схема модели приведена на рис. 2.8 а.

В качестве возможных вариантов ориентации зерна относительно по­ликристалла рассматривались три: контакт зерна с поликристаллом по вер­шине зерна (точечный контакт), ребру (линейный контакт) и плоскости (пло­ский контакт-имитация площадки износа на зерне). При изучении совмест­ной работы зерен рассматривались различные соотношения этих вариантов.

Конечноэлементный анализ проводился с применением восьмиузло­вых элементов SOLID.

Нагружение модели производилось по двум вариантам: 1) заданием перемещения Uy верхней плоскости связки (кинематическое воздействие —

имитация поперечной подачи STOa); 2) приложением давления к верхней плоскости связки (силовое воздействие нормальной и тангенциальной со­ставляющих силы резания — имитация упругой схемы шлифования). Досто­инством такого подхода является возможность изучения 3D НДС при упру­гой и жесткой схеме шлифования и сравнения результатов исследований.

Рис. 2.7. икни программы для расчета по методу конечных зле мент о а

 

Рис. 2.8. 3D модель напряженно-деформированного состояния системы «СТМ-зерно-связка»: а — конечноэлементная сетка системы «СТМ-зерно-связка»; б — конечно—элементная сетка зерна; в — деформации в системе; г — напряжения в СТМ; д, е — напряжения в зерне

со

В качестве характерной реакции модели на нагружение были приняты: 1) перемещение среднего узла верхней поверхности связки (величина попе­речной подачи) — Uув; 2) перемещение верхнего узла зерна (заглубление зер­на в связку) — Uу, 3) перемещение узла контакта зерна с поликристаллом

(упругое заглубление зерна в СТМ) — U™; 4) приведенные напряжения (по Мизесу) в верхнем узле контакта зерна со связкой — асв; 5) приведенные на­пряжения в узле контакта зерна с поликристаллом — апк.

Трехмерное изучение модели (по сравнению с плоской задачей) позво­ляет в нашем случае вскрыть существенную разницу в НДС при контакте зерна с СТМ по ребру и вершиной (в плоской задаче величина НДС будет одинакова). Сравнительный анализ результатов расчета НДС системы для плоской и трехмерной задачи показал, что они могут отличаться на 20-150 %. Естественно, что наиболее реалистичные результаты получаются при 3D моделировании.

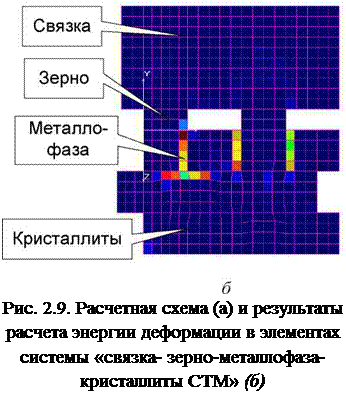
Поскольку в реальном процессе алмазного шлифования рассматривае­мая техническая система нагружена не только силовыми, но и температур­ными воздействиями, определяли величину главных и приведенных напря­жений, а также величину деформаций, энергии и плотности энергии дефор­мации в каждом элементе системы «СТМ-зерно-связка» от силового, темпе­ратурного и суммарного — термосилового нагружения. Для этого кроме ве­личины нормального давления или поперечной подачи задавалась и величи­на контактной температуры в зоне шлифования, и температура подаваемой в зону шлифования СОТС. При исследовании причин образования дефектного слоя (брака при шлифовании СТМ) поликристалл моделировался в виде со­вокупности отдельных кристаллитов и прослоек металлофазы. Пример ре­зультатов расчета термосиловых полей плотности энергии деформации в системе приведен на рис. 2.9.

Для определения объемов разрушенных СТМ и алмазных зерен ис­пользовали как силовые (приведенные напряжения превышают предел проч­ности СТМ на растяжение), так и энергетические (энергия деформации в элементе превышает предельное значение) критерии разрушения. Пакет по­зволяет определять величину энергии деформации и плотность энергии в

каждом элементе системы. При этом можно определить объем элементов с закритическими значениями приведенных напряжений или закритической энергией деформации. Эти возможности пакета использованы нами при тео­ретическом определении величины удельного износа в теоретическом моду­ле экспертной системы процесса алмазного шлифования СТМ (см. гл. 8).

Р + Т

SED

1 .4307000 1 .2525000

I

I.0743000 0.8980800 0.7178300 0.5398900 0.3814900 0.1833000 0.0051004

С целью получения максимально достоверных результатов расчета объемов разрушенных СТМ и алмазных зерен конечноэлементная сетка эле­ментов системы «СТМ-зерно-связка» сгущалась по мере приближения к зо­не контакта (к зоне разрушения) до размеров объема элемента, не превы — -4 3

шающего 10 мкм, что значительно меньше реально разрушаемого объема при одноактном воздействии алмазным зерном в процессе шлифования.

Возможности пакета по определению частоты собственных колебаний алмазных зерен в связке использованы нами для учета анизотропии физико­механических свойств СТМ при назначении оптимальных режимов шлифо­вания (см. п. 7.6).