Substituting s = jm in Equation 19.76, it is possible to solve the characteristic equation to find the unstable limit frequencies and the corresponding limits of grinding force stiffness at the threshold of instability. Noting that m = n. Q., the frequencies are given by
where A and B are the real and imginary parts of the geometric function as previously defined and
The limiting value is termed (k /Я0) and for various values of n is given by
![]() (19.80)
(19.80)
For integer values of n, stability and instability are independent of the grinding force and stability depends only on geometric stability. For near-integer values of n, the limiting value of (ks /Я0)* approaches infinity.
For half-integer values of n, the frequency is given by
It is essential to know whether the stable region is for values of ks/Я0 less than or greater than a limiting value (ks/Я0)*. This can be discovered by checking the phase angle % between the waviness r(t) and the deflection x(t). The system is unstable for ks/Я0 > (ks/Я0) * if
-П <X<+n (19.82)
where
X = 3 п/2-ф-п• n (19.83)
 |
|
and
![]()
|
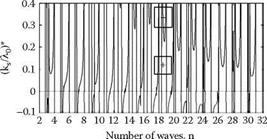
When X is less than 90°, deflection increases waviness. This means increasing grinding force increases waviness and the system becomes dynamically unstable.
