It has been shown that the effect of resonance is to destabilize the process. It has also been argued that static compliance can reduce growth rate of regenerative vibration. In this context, we are referring to static compliance that does not contribute toward a resonance. The resonance of a machine is the combined effect of a substantial mass and the supporting stiffness of the structure. However, it is possible to incorporate compliance at the grinding point by making the abrasive structure of the grinding wheel compliant. This does not affect the dominant tuning fork mode of the machine.
If the workpiece has low mass, compliance can also be incorporated at the control wheel surface without affecting the primary resonance. In fact, the soft rubber control wheel fulfills this function.
 |
An explanation for the stabilizing effect of added compliance is that the frequency response function of the machine is shifted to the right on the real axis. When the machine response function is added to the other terms in the characteristic equation, the shift to the right reduces the probability of enclosing the origin.
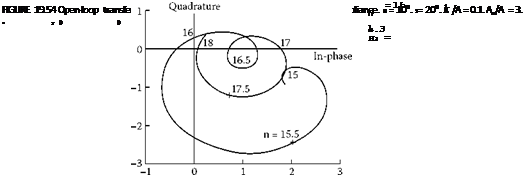
Additional static compliance can be demonstrated mathematically by introducing a secondary compliance term 1/A2 into the characteristic equation. Making the secondary compliance three times larger than the basic machine compliance changes the transfer function to that shown in Figure 19.54. This may be compared with Figure 19.53.
It can be seen that the additional compliance has stabilized the loop between 17.5 and 18 waves that was previously unstable. However, it is also found that while additional compliance reduces the growth rate at 16 waves, the instability cannot be overcome.
