The effect of the frequency response function for machine system compliances can be demonstrated using a second-order single degree of freedom system defined by
![]() A0 A0 x( jm) = 1
A0 A0 x( jm) = 1
A( jm) Fn (jm) 1 — eL + j-
E Qm0
where
is the undamped natural frequency.
is the dynamic magnification. Q is an inverse measure of damping c.
A frequency response function of a machine is shown in Figure 19.52 for a single mode of vibration. The frequency is expressed in number of waves for a particular workpiece speed by writing n = m/Q, as previously. The natural frequency of the machine in this case coincides with 17 waves. This corresponds to a natural frequency of 68 Hz in the tuning fork mode for a workpiece rotational speed of 4 Hz. The machine is lightly damped as indicated by the dynamic magnifier, Q = 10, a value that corresponds to a critical damping ratio of 0.05. This amplifies the static deflection by a factor of 10 at the resonant frequency.
![]()
![]()
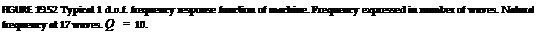
 17
17
 |
|
The characteristic equation for the grinding process including the dynamic response of the principal vibration mode is
Plotting the characteristic equation of the system for frequencies in the vicinity of the natural frequency for the unstable 16-wave geometry yields Figure 19.53. In this example, the natural frequency is at 16 waves. This result demonstrates the interaction between the large deflections of the machine at the frequency corresponding to 16 waves with the geometric instability at 16 waves. It is seen that frequency at 16 waves remains unstable but the main frequency of the instability is slightly below 16 waves.
Although the static compliance in Figure 19.53 is much lower than in Figure 19.51, the deflections of the dynamic system are much larger due to the resonance. The loop between 17.5 and 18 waves was previously stable with static compliance but has become unstable due to the nearby resonance at n = 16.
The situation of marginal geometric instability is often made worse by a resonance close to a frequency of marginal instability since resonance increases the probability of vibration amplitudes already in existence independent of the grinding process. These vibrations force a response even if the geometry is stable. The user should, therefore, consider a resonance in the same way as a frequency of forced vibration and avoid a coincidence with a convenient waviness. This may be achieved by adjusting the workspeed.
