Static compliance of the machine system is simply the inverse of static stiffness. Static compliance depends primarily on the elasticity of the wheels, bearings, slideways, and machine structure. System behavior, including the effect of static compliance, is similar to the results given by the simulations in Section 19.11. For this case
![]()
 |
H = —
a К
the open loop transfer function becomes
A high value of grinding force stiffness increases vibration deflections whereas a high value of system stiffness reduces them.
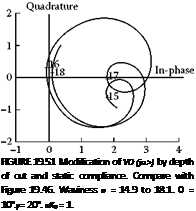 |
At the limit of stability, Equation 19.74 is equated to zero giving an equation of the same form as Equation 19.69. Figure 19.51 shows the effect of the geometric function modified by static
compliance and the depth of cut function. The sizes and positions of the circular loops are modified from the values in Figure 19.46 by the depth of cut function. The extent of the modification depends on the magnitude of kj Я0.
It is found that static compliance slightly reduces the growth rate at frequencies close to 16 waves but cannot make the situation stable. The most significant change from Figure 19.46 can be seen from the dimensions on the axes. Due to compliance, the deflections are greatly increased in magnitude.
