The Nyquist Criterion can conveniently be employed to test for stability. The Nyquist Criterion states that a system will be unstable if the open-loop transfer function encircles the point (-1, 0) on the negative real axis in a clockwise direction. With a small modification, the test may also be applied to the characteristic equation; the characteristic equation being the denominator of the closed-loop transfer function set to zero. In this case, instability is indicated by encirclement of the origin (0, 0) instead of the (-1, 0) point.
It can be seen that the term Gg (s) ■ Ha (s) features in both the work-regenerative and the wheel — regenerative loop transfer functions. It is, therefore, important in avoiding instability to ensure that this term is stable. The frequency characteristics of the functions can be explored in the usual way by substituting s = j®.
The following paragraphs explore the stability problem using Nyquist diagrams. Nyquist diagrams are used for simplicity compared to other methods.
19.12.3 The Depth of Cut Function
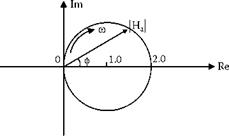
The depth of cut function Ha(j®) = 1 — cos ®T + j ■ sin®T is a circle of unit radius centered at the point (1, 0) on the real axis as the term ®T is varied from 0 to 2nn as illustrated in Figure 19.44. The period T is related to the workpiece rotational frequency Q expressed in radians per second by T = 2n/Q. The number of waves is given by n = ®/Q, leading to the function Ha (j ■ n) = 1 — cos2nn + j■ sin2nn.
The function has real values at 0 and +2. The real axis represents in-phase depth of cut. The point where the locus crosses the real axis at 0 is an integer wave condition where the new wave r(в) is in phase with the old wave r(в — 2n) passing the grinding point one revolution earlier. For a constant in-phase amplitude of waviness, excitation of the grinding force is zero. This condition occurs with convenient waviness. Excitation of the force is zero for a large waviness. For integer waves, the compliances and forces have no effect on limiting stability.
|
FIGURE 19.44 The frequency characteristics of the depth of cut function. |
The point where the locus crosses the real axis at +2 corresponds to the half-integer wave condition where the new wave is exactly 180° out of phase with the old wave. This condition causes a depth of cut amplitude that is double the amplitude of the wave. Instability at frequencies close to this condition corresponds to the harsh nature of chatter experienced in cutting and milling operations. Excitation of the chatter force may be large compared to the case of convenient waviness.