7. ОПТИМИЗАЦИЯ УИРАВЛЕИИЯ КАЧЕСТВОМ ПРИ ШЛИФОВАНИИ
7Л. Анализ технологического процесса шлифования как системы управления качеством
Конечной целью анализа пространственно-временного взаимодействия инструмента и обрабатываемой поверхности является синтез эффективных технологических процессов и управление ими в конкретных производственных условиях. Задача по разработке технологических процессов всегда является многовариантной. Как правило, существует несколько комбинаций характеристик инструмента, режимов резания, СОТС, обеспечивающих заданные параметры качества детали. С точки зрения экономики изготовление изделия должно вестись с минимальными затратами труда и минимальными издержками производства [21, 30, 34, 36, 45, 126, 101, 138].
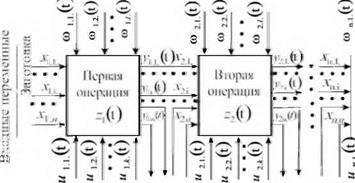
Технологический процесс может содержать одну или несколько операций шлифования. В последнем случае при решении задач оптимизации целесообразно объединять операции в более крупные технические системы (рис.7.1) [65]. Множество входных и выходных переменных всей системы включает при этом входные и выходные переменные каждой из подсистем за исключением связей, которые замыкаются внутри самой системы. К ним относятся параметры качества заготовки (объекта производства) после первой, второй, п-1- й операций. Параметры качества операнда (заготовка — деталь) являются связующим звеном не только отдельной операции, но и технологического процесса в целом. Выходные переменные качества после выполнения первой операции являются частью вектора входных переменных для второй операции, выходные параметры качества
после второй операции — частью входных переменных для третьей операции и т. д.
![]()
![]()
![]()
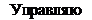
 U« ШIIUUOIIICC
U« ШIIUUOIIICC
ticn№
|
" з
|
Управляю шее ік> пенсійне
Рисунок 7.1 — Схема технологического процесса шлифования как
дискретной системы управления качеством
Представление совокупности технологических операций как системы управления является наглядной иллюстрацией принципа технологической наследственности. Анализ схемы технологического процесса (см. рис.7.1) показывает, что изменение входных параметров качества на первой операции при сохранении неизменными остальных переменных может привести к изменению параметров качества во всех звеньях системы и параметров качества на заключительной операции.
Анализ технологического процесса обработки заготовок абразивными инструментами как динамической системы позволяет наметить пути его оптимизации. Одной из основных особенностей любого технологического процесса механической обработки заготовок является дискретность. Технологический процесс состоит из отдельных операций, которые разделены во времени и пространстве. Операции выполняются на различном оборудовании, каждая из них определяется своим набором входных переменных, управляющих и
возмущающих воздействий, отличается специфическими закономерностями преобразования параметров качества объекта производства. Дискретность технологического процесса позволяет представить модель преобразования качества при выполнении і — й операции в виде системы уравнений [15] .
где yf — значение к — го параметра качества в момент времени t при
выполнении / — й операции; //’ — функция преобразования параметра качества на / — той операции; Ui (/) — вектор управляющих воздействий, в состав которого включены и входные переменные; С2/ (/) — вектор
случайных отклонений переменных (возмущающее воздействие).
Параметры качества (фазовые координаты объекта) после выполнения / — той операции зависят от алгоритмов изменения управляющих воздействий, состава возмущающих воздействий и состояния объекта после выполнения предшествующей операции.
Значения управляющих параметров в уравнениях (7.1) могут мен няться в определенных границах. Для каждой точки фазового пространства Y є Е и каждого фиксированного момента времени t
1 2 г
для вектора переменных задается некоторое непустое
множество Uj{Y(t — А/)), которое определяет допустимую область управления — пределы изменения управляющих воздействий
(7.2)
Для характеристики процесса на основании экономического принципа необходимо иметь также определенный показатель. В качестве критерия эффективности при проектировании операций обычно принимают либо приведенные затраты, либо себестоимость, либо трудоемкость изготовления детали [30,126]. Зависимость критерия эффективности от технологических факторов может быть выражена в виде функционала:
‘=/?(ад(0)+/°0іДМ0)+-+
„ (7.3)
+ /;? (П,-1,и„ (0) + G = Z)7(Y,_ 1 ,U;(0) + G.
/=1
где /-0 — функция критерия эффективности на / — й операции; G — сумма постоянных расходов, не зависящих от условий выполнения операций.
На основании рассмотренных связей задача оптимизации технологического процесса шлифования может быть сформулирована еле — дующим образом: зная начальное У{) и конечное Yn состояния,
выбрать такое допустимое управление (7.2) для объекта (7.1), которое придает функционалу (7.3) минимальное значение. Данная задача является задачей теории оптимального управления дискретными системами. Для её решения в явном виде необходимо выразить соотношения (7.1), (7.2) и (7.3) в виде зависимостей параметров от технологических факторов, определяющих процесс образования поверхности.
Представление технологического процесса обработки заготовок абразивными инструментами в виде динамической системы позволяет рассмотреть последовательность их оптимизации. В соответствии со схемой процесса преобразования параметров объекта (см. рис.7.1) могут быть намечены следующие основные этапы проектирования процессов чистового и тонкого шлифования: I) выделение из технологического процесса операций шлифования с определением начальных и конечных значений параметров качества; 2) выбор числа операций шлифования заготовки и определение оптимальных значений параметров качества после каждой из них; 3) выбор станков, характеристик инструментов, СОТС; 4) расчет режимов и высокопроизводительных циклов шлифования.
Первый этап — выделение из технологического процесса операций шлифования — выполняется по общим методикам проектирования технологических процессов на основании сопоставления себестоимости и трудоемкости с себестоимостью и трудоемкостью обработки заготовок другими приемлемыми методами [Ю, 45].
Второй этап — оптимизация маршрута технологического процесса — может быть выполнен путем структурной оптимизации методами теории оптимального управления дискретными системами [15, 16, 45] .
Выбор метода оптимизации отдельных технологических операций зависит от особенностей математической модели. Шлифованию свойственны признаки как непрерывных, так и дискретных процессов. Абразивный круг и заготовка при шлифовании вращаются и перемещаются непрерывно, инструмент находится в относительно постоянном контакте с обрабатываемой поверхностью, в течение всего цикла изменяются размеры, шероховатость, физикомеханическое состояние поверхностного слоя заготовки. Перечисленные признаки, однако, полностью не определяют закономерности образования поверхностей. При анализе изменений параметров качества базовых участков поверхности, целесообразно рассматривать шлифование как процесс дискретный.
Операции круглого наружного, внутреннего, плоского шлифования состоят из отдельных проходов (оборотов). Параметры качества базовых участков, текущий радиус-вектор заготовки изменяются не непрерывно, а периодически только при контакте поверхности с инструментом. После 7-го прохода они определяются параметрами качества после у-1-го прохода, режимом резания, состоянием рабочей поверхности абразивного инструмента. В пределах одного контакта базового участка поверхности с кругом режим резания либо сохраняется постоянным, либо изменяется незначительно.
Представление операции, как и всего технологического процесса в целом, в виде дискретной системы обусловливает возможность применения однотипных алгоритмов при решении задач структурной и параметрической оптимизации. При синтезе дискретных систем в настоящее время наиболее широко применяют
метод динамического программирования и метод локальных сечений
[15,16, 45].
При оптимизации отдельных технологических операций, когда U(/) = const и значения параметра качества на / — м этапе процесса не
зависят от значения параметра на /-1-м этапе, могут быть применены методы: линейного, геометрического и криволинейного программирования [30, 35, 98, 126]. Использование метода линейного программирования для оптимизации режимов шлифования рассмотрено в работах Г. К. Горанского [35], А. Н. Резникова [1], П. И. Ягцерицына [148], метода криволинейного программирования — в работах В. А. Глаговского, В. Л. Акимова, З. И. Кремня [30], метода динамического программирования для оптимизации стойкости абразивного инструмента и оптимизации процесса доводки — в работе П. Н.Орлова, Ю. И.Нестерова, В. А. Полухина [103].
Основной принцип динамического программирования заключается в том, что каковы бы ни были первоначальное решение и первоначальное состояние объекта, последующие решения должны определять оптимальную стратегию относительно всех состояний, полученных в результате первоначального решения [15]. Сущность метода динамического программирования состоит в том, что для оптимальности всего процесса в целом нужно, чтобы на каждой промежуточной стадии последующая часть процесса также обладала свойством оптимальности.
При решении задачи методом динамического программирования уравнение для критерия эффективности (7.3) может быть преобразовано в рекуррентное соотношение:
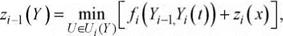 (7.4)
(7.4)
где Zj (Y ) и Zj_і (К) — наименьшее значение критерия эффективности
на заключительном этапе технологического процесса после / — й и / — 1 — й операций.
При оптимизации процессов обработки заготовок абразивными инструментами представляется возможным применять метод динамического программирования для назначения маршрута
технологического процесса и условий выполнения отдельных операции. Для решения поставленной задачи необходима разработка оптимизационных моделей и алгоритмов. С учетом наиболее важных параметров качества таких, как величина радиус-вектора, пространственные отклонения, глубина дефектного слоя и шероховатость поверхности объекта система (7.1) в общем виде записывается:
где /у и /’_! — радиус-вектора поверхности после выполнения / — и и / -1-й операций; А/-. — радиальный съем металла на j-м проходе (обороте) при выполнении / — й операции; 8 , — пространственные отклонения после / — й операции; Аб^ — пространственные отклонения,
удаляемые на j-м проходе (обороте) при выполнении / — й операции; 8npj — пространственные отклонения, вносимые /—й операцией;
7у,, Н р — глубина дефектного слоя и шероховатость поверхности, возникающие на / — й операции.
В качестве критерия эффективности в общем случае принимают приведенные затраты на единицу продукции, которые вычисляют по формуле:
3 = С+ЕНК,
где С — себестоимость единицы продукции; К — удельные капитальные вложения в производственные фонды; Ен — нормативный коэффициент капитальных вложений.
Себестоимость единицы продукции при выборе варианта технологического процесса целесообразно определять методами прямого распределения затрат (метод калькулирования). При оптимизации режимов резания и оценке этапов высокопроизводительных циклов М. М. Тверским [128] в качестве критерия эффективности рекомендуется принимать приведенные затраты на удаление единицы объема материала. Минимум приведенных затрат достигается при следующем значении
интенсивности съема материала
где Ст и к — коэффициент и показатель степени в уравнении периода стойкости от интенсивности съема материала Tu =Ст время на смену круга и суммарное время, расходуемое на все правки; И — стоимость абразивного инструмента.
Для ряда технологических процессов чистового и тонкого шлифования до 80% переменной доли себестоимости
пропорционально штучному времени выполнения операции [99] , что позволяет при наложении ограничения на капитальные затраты выполнять оптимизацию по быстродействию. Критерий эффективности — штучное время выполнения і — й операции — вычисляется при этом по объему материала, который необходимо удалить с поверхности Qni, и интенсивности его съема Q
где кп — коэффициент, учитывающий влияние на основное время пути врезания и схода инструмента; Тдап — сумма дополнительных затрат времени; Ь0 — длина обрабатываемой поверхности; /7, — припуск на шлифование.
Начальное состояние объекта характеризуется системой неравенств
Анализ систем (7.5), (7.8) и (7.9) показывает, что для расчета оптимальных процессов шлифования необходимо иметь аналитические зависимости изменения размеров, отклонений формы, параметров шероховатости обрабатываемой поверхности, физикомеханического состояния поверхностного слоя. В предлагаемой работе рассмотрен пример, отражающий только часть функционалов комплексной математической модели, что не позволяет выполнять полную оптимизацию процессов образования поверхностей. В то же время на основе предложенных моделей может быть успешно решен ряд этапов синтеза операций чистового и тонкого шлифования, когда лимитирующим параметром качества является шероховатость поверхности.
В связи с тем, что структурная оптимизация обычно выполняется на основе оптимизации параметрической, далее последовательно решаются вопросы определения характеристик инструмента, режимов резания, числа операций чистового и тонкого шлифования. На каждом из этапов рассматривается общая постановка задачи, а затем дается её частное решение при проектировании процессов с обеспечением заданных параметров шероховатости поверхности.
