Отклонения формы шлифованных поверхностей достаточно часто определяют долговечность и точность работы узлов деталей машин и приборов. Они меняют характер посадок, снижают точность подвижных соединений, точность взаимного расположения поверхностей, уменьшают площадь контакта и жесткость соединений, увеличивают уровень вибраций, шум в машинах, снижают герметичность соединений [38, 40, 127].
При проектировании операций шлифования обеспечение требуемой величины отклонений формы часто вызывает большие трудности, чем обеспечение требуемого допуска на размер. Точность размеров достигается при шлифовании за счет повышения точности оборудования и средств активного контроля, системы же автоматического управления и контроля отклонениями формы достаточно сложны и не получили широкого распространения. Особое внимание управлению радиальным биением, овальностью, огранкой, волнистостью уделяется при обработке деталей подшипников, топливной аппаратуры, шпинделей металлорежущих станков, валов турбин. Допуск на отклонение формы при обработке этих деталей может составлять до 60% от допуска на размер, а требуемые отклонения от округлости достигают от 0,2 до 2 мкм.
Основными причинами появления отклонений формы в продольном сечении цилиндрических поверхностей являются упругие деформации в технологической системе, неравномерность износа абразивного инструмента, винтовое движение инструмента относительно обрабатываемой поверхности. Основными причинами отклонений формы в поперечном сечении являются погрешности установки, исходные отклонения формы заготовки, волнистость рабочей поверхности инструмента, погрешности базовых поверхностей, собственные, вынужденные, параметрические и автоколебания, возникающие в технологической системе [46, 50, 127].
При расчете точности на операциях круглого шлифования в центрах погрешность базирования гь принимается равной нулю, а погрешность закрепления — пропорциональной составляющей силы резания, по направлению которой определяется смещение. Амплитуды погрешностей формы, переносимых с центрового отверстия, принимаются пропорциональными модулю комплексного числа, определяемого механическими импедансами заготовки и шлифовального круга.
Для вычисления погрешностей обработки, связанных с упругими отжатиями в технологической системе, существует количественное выражение: сила — податливость. По данным
исследований К. С. Ко лева, динамическая жесткость станка значительно отличается от статической [50]. Для характеристики системы в рабочем состоянии вводится динамический коэффициент Цд, который определяется опытным путем. При расчете остаточной погрешности используют эмпирические зависимости, связывающие радиальный съем материала с радиальной составляющей силы резания.
Наиболее значительны при шлифовании отклонения формы, вызванные вибрациями в технологической системе. Детальный обзор исследований, выполненных в области анализа влияния
технологических факторов на волнистость шлифованной поверхности, проведен в работе В. А. Прилуцкого [112]. Основные исходные моменты существующих методик расчета волнистости сводятся к вычислению переменной составляющей силы резания, составлению и решению дифференциальных уравнений, определяющих взаимное расположение заготовки и инструмента, расчету амплитуды, профиля и высоты волны обработанной поверхности. Радиальная составляющая силы резания обычно определяется по эмпирическим зависимостям, а величина волнистости обработанной поверхности принимается равной волнистости условной границы поверхностей резания (воспроизводящего поля) Wp. Такое допущение является
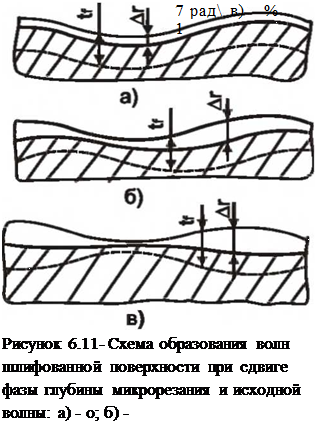
справедливым для процессов предварительного и чернового шлифования. Более точно высота образующейся волнистости Wu, рис. 6.11, может быть определена по зависимости, учитывающей различие размеров слоя шероховатости во впадинах и на вершинах волны,
К=^р-(Нт-Нвыс), (6.17)
где Нвп и Нвыс — размеры слоя шероховатости (переходного слоя материал — среда) во впадинах и на вершинах волны.
Для процессов чистового и тонкого шлифования слой шероховатости поверхности во впадинах может быть в 1,2… 1,5 раза больше чем на ее выступах (см. рис. 4.27). При амплитуде изменений глубины резания А, =0,5tj и отсутствии самоперерезания волн
волнистость условной границы воспроизводящего поля в уравнении (6.17) равна tj, а толщина слоя шероховатости — (0,75…0,85) tj (см табл. 4.1). Таким образом, вычитаемое {Нвп- Нвыс) может составлять
 |
от 40 до 60% от расчетной высоты волнистости и поправка, вносимая уравнением (6.17), для процессов чистового и тонкого шлифования является весьма существенной.
Вычисление отклонений формы по зависимостям вида (6.17) приводит к определению координат точек обработанной поверхности
детали по координатам точек исходной поверхности заготовки и величине съема материала. Для процесса круглого наружного шлифования задача сводится к вычислению текущего радиус-вектора обрабатываемой поверхности после первого, второго и т. д. контактов с инструментом. В общей постановке при исследовании механизма образования отклонений формы необходимо рассматривать взаимодействие двух случайных, упруго деформируемых поверхностей — заготовки и инструмента. Полная статистическая оценка параметров отклонений формы в поперечном сечении может быть выполнена методами имитационного моделирования. Подобный подход к анализу отклонений рассматривается в работах Е. Ю. Татаркина [95]. В выполненных исследованиях дается общая постановка вопроса и примеры решения конкретных задач. Как и при анализе закономерностей удаления материала предполагается, что уравнения движений для технологической системы составлены и решены до уровня определения координат центров вращения инструмента и заготовки.
 Рассмотрим более
Рассмотрим более
детально закономерности
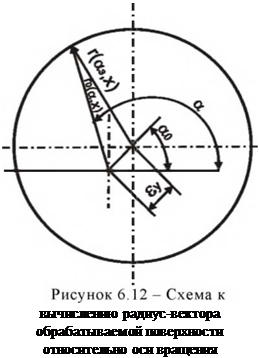
изменения геометрических параметров (размеров и формы) поверхностей при круглом наружном шлифовании, рис. 6.12. Исходный радиус-вектор заготовки в цилиндрических координатах с полюсом, совмещенным с
конструкторской осью, в работах А. В. Гаврилова и Л. К. Сизенова записывается случайной функцией полярного угла а [130]
r0(a, x) = r0(x) +
p, (6.18)
+ Z Ak cos(£a + v|/ £)
k=l
где г0(х) — радиус средней окружности сечения поверхности заготовки на расстоянии х от базовой поверхности, например торца заготовки; Ак и \i к — амплитуда и фаза отклонений к — й гармоники.
Погрешности с порядком к= 1 определяют отклонения расположения поверхности (эксцентриситет) относительно конструкторской оси. Погрешности с порядковым номером к = р + 1 VL более характеризуют микрорельеф поверхности.
Суммарное поле рассеивания погрешности радиус — вектора отклонений размеров и формы партии заготовок вычисляется по зависимости
![]() 2
2
![]()
где CT;j) — дисперсия отклонении среднего радиус
амплитуды.
При установке заготовок на станок возникают погрешности базирования и закрепления (см. рис. 6.12). Вследствие этого ось вращения поверхности не совпадает с конструкторской осью. Пересчет радиус — векторов выполняется по общим уравнениям окружности в полярных координатах
9 9 9
r0 (a, x) + 2r0(a, x)evcos(a — a0) + sv =r (а3,х), (6.19)
где г0(а, х) — радиус-вектор установленной на станок заготовки, измеряемый от центра ее вращения; є v, — векторная сумма эксцентриситета заготовки и погрешности ее установки в радиальном направлении; а0 — угол между осью у и прямой, соединяющей центр вращения заготовки с конструкторской осью.
В процессе шлифования изменения радиуовектора и отклонений формы поверхности оцениваются относительно оси
вращения заготовки. После окончания обработки переход к анализу отклонений относительно конструкторской оси выполняется по зависимости (6.19).
Для вычисления текущего радиус-вектора обрабатываемой поверхности воспользуемся соотношением (3.39), которое для двух последовательных контактов (проходов) принимает вид
Vj (а, х) = j (а, х) — Arf (а, х) + Дгф (а, х), (6.20)
где Л/у (а, х) и Arqj (а, х) — радиальный съем материала и
температурные деформации заготовки при j — м контакте поверхности с инструментом.
В уравнении (6.20) Аг определено для любых значений lj с
учетом упругих, температурных деформаций и вибраций в технологической системе. По радиус-вектору заготовки может быть рассчитан радиус-вектор поверхности после первого контакта, по радиус-вектору после первого контакта — радиус-вектор после второго контакта и т. д.
Суммарные отклонения формы и расположения относительно центра вращения заготовки вычисляются по наименышму и наибольшему значениям радиус-вектора поверхности
где 5 j — пространственные отклонения поверхности после j — го прохода; гтах • и гтт • — соответственно максимальное и минимальное
значения радиус-вектора заготовки после j — го прохода (оборота).
Объединяя уравнение (6.21) с уравнениями (6.20) (4.44), (4.12), (2.27), (5.19) получим систему для расчета отклонений формы обработанной поверхности
где радиальный съем металла на j — м обороте вычисляется решением третьего уравнения при значении t. j из четвертого уравнения системы.
Решение системы уравнений (6.22) возможно на ЭВМ с применением методов имитационного моделирования. Упрощенное решение может быть получено либо для отдельных реализаций профилей заготовок и инструмента, либо при условии аддитивности отдельных слагаемых погрешности.
Система (6.22), исключая первое уравнение, определяет изменение радиус-вектора заготовки в любой точке обрабатываемой поверхности и позволяет рассчитать как остаточные отклонения, так и вносимые самим процессом формообразования.
Частота гармоник остаточных отклонений, уравнение (6.18), как правило, бывает меньше частоты собственных колебаний технологической системы, что позволяет при анализе опускать гармоники высших частот и анализировать их влияние на процесс
отдельно. Вычисление упругих деформаций элементов
технологической системы может быть заменено на определение суммарных деформаций по силам резания и податливости системы
П
mTS. Из этого следует, что ^ Дyvk = mTSAPv. При частных значениях
к=
коэффициентов х =1,5; т= 0,5; z= 5 и достаточно плавном изменении режима резания система для расчета остаточных суммарных отклонений формы и расположения поверхностей принимает вид
.
Циклограмма изменения радиус-вектора поверхности в точке выхода из зоны контакта заготовки с кругом для случая шлифования образцов из нормализованной стали диаметром 50 мм кругами 1 — 300x40x127 24А 25-Н СМ2 5К при скорости круга 35 м/с, скорости заготовки 0,25 м/с, поперечной подаче 0,01 мм/об приводится на рис. 6.13. Величина эксцентриситета заготовки принята равной 0,1 мм.
В первый период процесса заготовка, имеющая эксцентриситет, касается круга только на участках с максимальным припуском, металл
даляется с одной стороны, за счет этого величина пространственных отклонений уменьшается. Во второй период обрабатываемый материал снимается как со стороны наибольшего припуска, так и со стороны наименьшего припуска, но величина пространственных отклонений продолжает уменьшаться за счет разности в радиальном съеме металла.
Для вычисления остаточных пространственных отклонений по системе (6.23) выполняется последовательный анализ изменения величин радиус-векторов со стороны наибольшего и наименьшего припусков. Для этого из условия tf > 0 проверяется наличие контакта
поверхности с инструментом. Для контактирующих участков по четвертому уравнению системы вычисляется приращение глубины микрорезания, по глубине микрорезания определяется радиальный съем материала. По первому уравнению вычисляется остаточное пространственное отклонение.
Пример аналитического расчета изменения пространственных отклонений для рассмотренного ранее процесса врезного шлифования образцов из стали приводится в табл. 6.2. Величина остаточных пространственных отклонений с увеличением времени шлифования закономерно уменьшается.
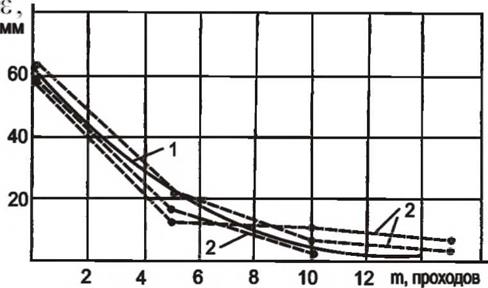
Аналогичная зависимость наблюдается и при шлифовании заготовок с продольной подачей, о чем свидетельствуют экспериментальные и расчетные данные, полученные для случая шлифования колец из стали 45 кругами 1-400x40x127 24А 25-Н СМ2 5К с продольной подачей 0,02м/с, поперечной подачей 0,04 мм/ход, рис 6.14. С увеличением числа проходов остаточный эксцентриситет є уменьшается, асимптотически приближаясь к нулю. Скорость его изменения увеличивается с повышением жесткости системы.
|
Рисунок 6.14 — Влияние числа проходов на эксцентриситет обрабатываемой поверхности при шлифовании образцов из закаленной стали 45 кругами 24А 25-Н СТЗ 7К при скорости круга 34 м/с, скорости заготовки 1 м/с, продольной подаче 0,033 м/с, поперечной подаче 0,02 мм/ход: 1 — расчетные данные; 2 — экспериментальные данные |
Из анализа расчетных и опытных данных по изменению величины остаточного эксцентриситета следует важный вывод о возможности управления точностью за счет дополнительного смещения поверхности относительно оси вращения в сторону увеличения эксцентриситета (материалы заявки № 26266873/08). При смещении поверхности увеличивается съем материала со стороны большего припуска и уменьшается со стороны меньшего припуска, за счет чего достигается увеличение скорости изменения величины остаточного эксцентриситета. Кривая, характеризующая изменение эксцентриситета в этом случае, при некотором значении времени обработки будет пересекать ось абсцисс. Эксцентриситет заготовки полностью будет устранен.
Экспериментальная проверка, выполненная в лабораторных условиях, показала, что при применении предложенного способа время обработки заготовки, имеющей исходный эксцентриситет, может быть уменьшено в 1,5…2 раза с обеспечением заданной точности обработки.
Полученные зависимости для расчета остаточных пространственных отклонений позволяют учесть влияние на процесс формирования параметров точности нелинейности в технологической системе.
Сопоставление данных расчетов с результатами определения пространственных отклонений позволяет сделать заключение, что наибольшее уточнение в расчетах достигается для условий повышенной жесткости системы. Для условий пониженной жесткости результаты отличаются незначительно.
Для аналитического расчета амплитуды отклонений формы высших гармоник выберем участок поверхности, по размерам соизмеримый с частотой вынужденных и собственных колебаний системы. Будем полагать также, что за время прохождения этого участка зоны контакта заготовки с кругом величина температурных деформаций системы и упругих деформаций станка и приспособления постоянны. В этом случае изменение межцентрового расстояния А будет определяться только вибрациями в технологической системе, а глубина микрорезания — межцентровым расстоянием, исходным радиус-вектором инструмента, величиной упругих деформаицй материала инструмента и заготовки.
Величина пространственных отклонений высших гармоник определится по разности наибольшего и наименьшего радиус — векторов в пределах выбранного участка.
|
Продолжение таблицы 6.2
|
Наиболее сложно вычисляется амплитуда волны при обработке поверхности в несколько проходов. В работе [112] показано, что при шлифовании совпадение фазы волны выполняемого и предшествующего оборота наблюдается только при синхронизации вращения заготовки с вращением инструмента. Иначе говоря, фазы гармоник колебаний центра вращения инструмента и профиля круга на выполняемом проходе не зависят от фазы исходной волнистости.
На рис. 6.11 приводится схема образования волн при
71
последовательных оборотах при сдвиге фаз 0; — и ж. Наиболее неблагоприятные условия наблюдаются при совпадении фаз. При
сдвиге фаз на — амплитуда результирующей волны уменьшается, еще
большее её снижение наблюдается при сдвиге фаз на половину периода.
Анализ полученных данных показывает также, что амплитуда волны по своему значению может быть меньше амплитуды колебаний не только для частот, при которых возникает явление самоперерезания волн, но и для частот, при которых это явление не имеет место. Уменьшение амплитуды волны связано с влиянием на точность упругих свойств связки инструмента [109]. С повышением податливости абразивного инструмента увеличиваются его упругие деформации в момент сближения оси круга и заготовки, вследствие этого изменения глубины микрорезания уменьшаются.
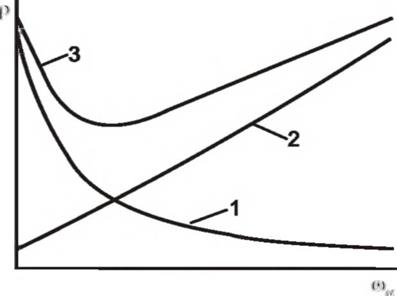
Полученные результаты позволяют обосновать выбор связки абразивного инструмента. По данным ВНИИАШ [6], круги, изготовленные на керамической, бакелитовой, глифталевой связках, в первую очередь отличаются по модулю упругости и податливости. С увеличением податливости абразивного инструмента со(} с одной стороны снижается волнистость поверхности (рис. 6.15, кривая 1), с другой стороны снижается жесткость системы, в результате чего увеличиваются остаточные пространственные отклонения (см. рис. 6.15, кривая 2). Суммарная погрешность в этом случае будет иметь минимум, который определяет оптимальные упругие свойства
абразивного инструмента. С увеличением амплитуды вибраций минимум кривых смещается в сторону снижения жесткости абразивного инструмента.
|
Рисунок 6.15 — Влияние податливости инструмента на пространственные отклонения р шлифованной поверхности |
Таким образом, для каждого процесса абразивный инструмент должен иметь оптимальные упругие свойства, обеспечивающие получение наименьших пространственных отклонений обработанной поверхности.
С увеличением жесткости и виброустойчивости станков целесообразно применять более жесткие круги. При уменьшении жесткости станка, приспособления, консольном закреплении заготовки целесообразно использовать более эластичные абразивные инструменты. Данный вывод подтверждается рекомендациями по выбору связки абразивного инструмента, которые составлены на основе обобщения опыта передовых предприятий [1, 6, 102]. В инструментальной, автотракторной, приборостроительной
промышленностях при шлифовании деталей в центрах, бесцентровом шлифовании применяются преимущественно круги на керамической связке, при шлифовании колец подшипников при консольном креплении заготовки — круги на вулканитовой связке.
Для процесса тонкого шлифования мелкозернистыми кругами целесообразно применять абразивные инструменты на керамической связке при обработке заготовок на станках повышенной и особовысокой точности, круги на органических связках — на станках нормальной точности. Примером успешного использования кругов на керамической связке является операция спаренного шлифования плунжеров топливного насоса из стали ШХ15 на станках PHU-500. При обработке кругами из карбида кремния зеленого 63С 4-Н С2 10К обеспечивается шероховатость поверхности Ra = 0,02…0,04 мкм, точность размера — 1 мкм, отклонения формы — 0,5 мкм, что позволяет в комплексе с другими операциями технологического процесса производить детали топливной аппаратуры из износостойких сталей и увеличить их долговечность. Мелкозернистые круги на органических связках успешно применяются при обработке деталей подшипников. Например, чистовое шлифование образующей бочкообразного ролика железнодорожных подшипников выполняют кругами на вулканитовой связке 63С 10-Н СТ В, шлифование торцов роликов — кругами из электрокорунда белого зернистостью 6-8 твердостью С-СТ2 десятой структуры на бакелитовой связке.