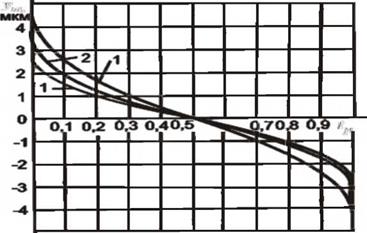
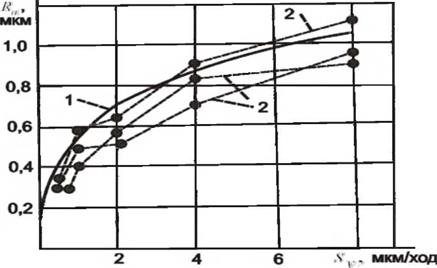
Микрорельеф шлифованной поверхности представляет собой совокупность отображений в материале заготовки поверхностей резания, образованных при движении режущих кромок инструмента в пространстве обрабатываемой заготовки. Форма единичных рисок будет определяться формой режущих кромок, особенностями контакта с материалом поверхности. Для каждого отдельного абразивного зерна практически невозможно предсказать, какова будет форма единичного среза, и оценить все возможные варианты среза. В тоже время с позиций теории вероятностей и случайных процессов (раздел 3) могут быть определены статистические оценки для параметров шероховатости шлифованной поверхности.
Аналитические зависимости для определения важнейших параметров шероховатости поверхности при условии, что случайный процесс, описывающий ординаты, является стационарным и нормальным, получены в работах Ю. В. Линника, А. П. Хусу и Ю. Р. Витенберга [66, 143, 24]. Параметры шероховатости вычислены по корреляционным функциям. Вид функции принимается известным, а её коэффициенты определяются на основе экспериментальных исследований процесса шлифования.
Основы прогнозирования важнейших параметров шероховатости поверхности по технологическим факторам рассмотрены в работах А. В. Королева [54] и в работах автора [92, 96, 97]. Известные зависимости могут быть существенно уточнены, если учесть влияние на неровности процессов, возникающих в динамической системе.
Расчет параметров шероховатости выполнен на основе функционалов, полученных при теоретическом анализе процессов формообразования поверхностей, в третьем разделе. Величина слоя, в котором распределена шероховатость поверхности, в общем слуше определяется решением уравнений (4.1) и (4.44) относительно Н = t. j — Аг при заданном уровне вероятности удаления материала.
Для установившегося процесса шлифования при частных значениях коэффициентов у и т величина слоя шероховатости поверхности вычисляется по зависимости (4.50). Математическое ожидание относительной опорной длины профиля определяется по вероятности неудаления материала по уравнению (3.21). Среднее арифметическое отклонение профиля R(l может быть вычислено по площади выступов
Fj и площади впадин Ь, измеренных от средней линии профиля (см. рис. 3.8 и уравнение (3.33)). Так как dFx = t Ldym и dF2 = (1 — t )Ldym, то
со 0
К = j tpdym + j (! — tp)<fym > (6-!)
0 — со
где L — длина базового участка, мм; ут — расстояние от точек профиля до его средней линии.
Зависимость для вычисления Ra значительно упрощается, если воспользоваться ранее рассмотренным положением, что случайный процесс, описывающий ординаты профиля, является стационарным и нормальным. Для такого процесса математическое ожидание среднего арифметического отклонения профиля пропорционально среднему квадратическому отклонению oYm случайных ординат Yт точек профиля
mw=J-m=°rJ-(6-2)
V я V п
где к(0) — значение корреляционной функции при интервале Х = х2 равно дисперсии случайной величины Ym.
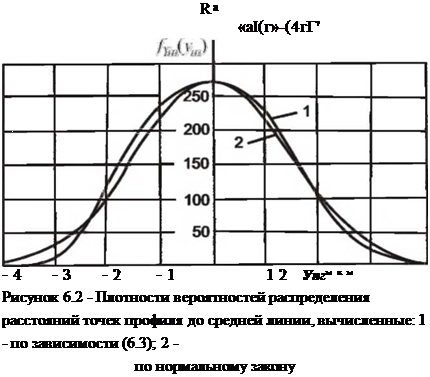
Для определения среднеквадратического отклонения а} т вычислим функцию /’},,,(ут) и плотность вероятностей расстояний Ут. Для положительных и отрицательных значений ут
Плотности вероятностей ординат профиля, вычисленные по уравнению (6.3) и закону Гаусса, приведены на рис. 6.2 (кривые 1 и 2). Почти полное их совпадение подтверждает гипотезу, что случайный процесс — ординаты шлифованной поверхности профиля — близок к нормальному. Для такого процесса при Ут = 0, ДМ) = 0,5,
fvm(Ут) =—- * /— . На основании этого вторая часть уравнения (6.3),
ауП12к
выделенная фигурными скобками, равна 0,5, а среднее арифметическое отклонение профиля, учитывая уравнение (6.2), определится как
 |
 |
Расстояние Wm от наиболее глубокой впадины до средней линии профиля вычисляется из условия ут = 0, Р(М) = 0,5,
(Wm — /’Ar)v — In 2 = 0.
?=о
При величине радиального съема металла Ar > Wn
W
‘ ‘ TV,
Для приближенных расчетов можно также принять tf — А г
—-—. При частных значениях т = 0,5, у = 1,5 зависимость (6.4) принимает вид:
Я
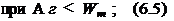
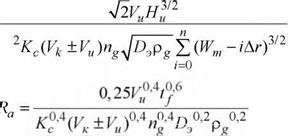Уравнение (6.6) по своей структуре и величине показателей степени при переменных факторах близко к имеющимся в литературе степенным зависимостям, но в отличие от них отражает физическую природу процесса формообразования и соответствует основным принципам теории размерностей.
 |
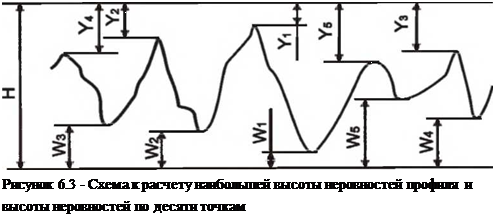Наибольшая высота неровностей профиля Rmas и высота неровностей профиля по десяти точкам Rz могут быть рассчитаны по величине слоя, в котором распределена шероховатость поверхности, и математическим ожиданием расстояний Yi, Y2…Y5 от верхней границы слоя до пяти высших точек профиля и расстояний Wi, W2…W5 от нижней границы слоя до пяти низших точек профиля, рис. 6.3.
Рассматриваемые расстояния являются величинами случайными и независимыми, на основании этого
М[/Єтах] = Я-А/[У1]-М[Ж1];
Для стационарного процесса, близкого к нормальному, реализацией которого являются нрофилограммы шлифованной поверхности, можно считать, что расстояния от верхней границы слоя шероховатости до наиболее выступающих вершин профиля распределены по законам, аналогичным распределению расстояний от впадин до нижней границы слоя. Из этого вытекает примерное равенство математических ожиданий и дисперсий Yi и Wt.
Если плотность распределения вершин зерен по глубине инструмента моделируется степенной зависимостью, то число вершин зерен, проходящих за последний контакт участка поверхности с кругом, определится из уравнения
Для вычисления математических ожиданий и дисперсий определены соответствующие функции распределения/д (w). Каждую из наиболее глубоких впадин микрорельефа можно рассматривать как след от отдельной вершины абразивного зерна,
поэтому вероятность событий P(Wx<w), P(W2<w),…,P(W5<w), заключающегося в том, что расстояния от нижней границы до первой, второй,,…, пятой впадин меньше некоторых фиксированных значений w, определяется вероятностью прохождения через слой сечения от w=0 до w соответственно не менее одной, двух,…, пяти вершин зерен. Вероятность прохождения через участок сечения длиной L хотя бы одной вершины определяется следствием закона Пуассона
Вероятность прохождения хотя бы двух вершин меньше вероятности прохождения хотя бы одной вершины на величину
вероятности прохождения только одной вершины
 |
 |
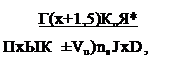(6.10)
Значения параметра Х при расчете вероятности удаления материала, математических ожиданий и дисперсии /і? тах и Rz могут
быть различны, поскольку моделируются разные участки действительной кривой плотности вероятности распределения зерен по глубине инструмента/(м). При частном значении у =1,5 уравнения (6.7) и (6.9) принимают вид
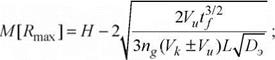
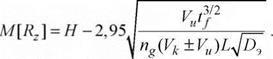(6.11)
(6.12)
В оптимальную систему характеристик шероховатости, кроме рассмотренных, входят параметры кривой опорной поверхности, расстояние от линии выступов до средней линии R относительная
опорная площадь на уровне средней линии tR [117]. При оценке
несущей способности шероховатости кривая опорной поверхности, построенная в относительных координатах, обычно описывается
уравнением tp=be‘p (є — относительное расстояние от линии выступов, є=7/ RmsK, где 7 — расстояние от линии выступов до рассматриваемого уровня). При выражении через технологические параметры коэффициенты аппроксимирующего уравнения кривой опорной поверхности легко получить методом наименьших квадратов, имея расчетные значения / . С достаточной точностью (±2,8%) они
могут быть определены также по двум, трем точкам действительной кривой. Так, расчетные значения / для точек с координатами
 |
7 = 0,25i? max и 7 = 0,5Rmax соответственно равны
 |
При вычислении по аппроксимирующему уравнению
t25=b(0,25)4 t50=b(0,5)4
По параметрам кривой опорной поверхности и среднему арифметическому отклонению профиля могут быть определены расстояние от линии выступов до средней линии и относительная опорная площадь на уровне средней линии
,. _ v’-+1 _д„(у„+і)
р 2 Ъ ’ Rp 2Rp ‘
Пример аналитического расчета высотных параметров шероховатости поверхности для процесса круглого наружного шлифования образцов из стали 9X2 диаметром 50 мм кругами 1- 300x40x127 24А 25-Н СМ2 4Б приводится в таблице 6.1. При расчетах принято: Кс= 0,9; Vk=35 м/с; Vu=0,25 м/с; п = 5,2 1/мм2;
pg =0,021 мм; tj =0,0116 мм; Аг = 3,3-10 мм; значение базовОй
длины L = 0,8 мм. Все расчеты выполнены с соблюдением размерностей, рекомендованных системой СИ. Например, число абразивных зерен на единице рабочей поверхности инструмента
6 2
принимается равным 5,2-10 1/м, радиус закругления при вершине
зерна — 21 -10—6 м.
Сопоставление расчетных и экспериментальных значений относительной опорной длины профиля для рассмотренных в примере условий шлифования приведено на рис. 6.4. Линии 1 ограничивают область, в которой разместились десять экспериментальных кривых при совмещении их точек со средней линией профиля. Вычисленные значения относительной опорной длины профиля для всех уровней не выходят за пределы разброса экспериментальных данных.
|
Рисунок 6.4 — Опорные кривые шлифованной поверхности: 1 — область экспериментальных значений; 2 — расчетные значения |
Аналогичные результаты получены по среднему арифметическому отклонению профиля при круглом наружном осциллирующем шлифовании с изменением поперечной подачи, рис. 6.5.
|
Рисунок 6.5 — Сопоставление расчетных (———— ) и экспериментальных (———— ) значений среднего арифметического отклонения профиля поверхности детали из стали 9X2, шлифованной кругом 24А 25-Н СМ2 4Б при: = 35 м/с; /= 0,25 м/с; Sx = 0,033 м/с |
Отмечается идентичность формы расчетных и экспериментальных кривых, отражающих влияние на шероховатость поперечной подачи Sv. Отклонения расчетных значений от
экспериментальных при всех значениях Sv не превышает 20%.
Подробный анализ адекватности моделей для расчета математических ожиданий наибольшей высоты неровностей профиля Rmas и высоты
неровностей профиля по десяти точкам R„ выполнен в работе [92].
Особенностью рассмотренных моделей является то, что при расчетах учитываются не только параметры режима резания, но и параметры состояния рабочей поверхности инструмента. При описании переходной области материал — среда вероятностью удаления и неудаления материала вычисляются все наиболее важные параметры шероховатости поверхности и корреляционная функция микропрофиля обработанной поверхности. Модель позволяет также оценить влияние на параметры шероховатости многопроходности процесса шлифования. При решении уравнений без учета и с учетом многопроходности для ранее рассмотренного примера величины слоя шероховатости поверхности соответственно равны 9,1 и 7,2 мкм. Уточнение значения слоя шероховатости поверхности при использовании модели составляет 11%. Для других режимов шлифования оно равно 5 — 25%, что является существенным в особенности при решении задач оптимального управления. Основные зависимости для расчета параметров шероховатости поверхности приведены для процесса круглого наружного шлифования, но аналогичные модели могут быть получены и для других операций обработки деталей абразивными инструментами, например, внутреннем, торцовом, плоском шлифовании.
В отличие от известных, предложенные зависимости позволяют также прогнозировать кинетику изменения параметров шероховатости. В уравнения (6.7), (6.8) и (6.9) неявно входит вероятность удаления материала, которая вычисляется с учетом шероховатости заготовки и ее изменений при каждом контакте поверхности с инструментом.