При шлифовании

Силы резания при шлифовании являются результатом упругопластического контакта с материалом абразивных зерен, связки и стружек, заполняющих поры круга, а также гидродинамических потоков. Величина радиальной 1, и тангенциальной Р2

составляющих сил могут быть рассчитаны по формулам [54]:

Р =Ур +Р +Р +Р ■

у Z-u gyi сеу сту ggy ’

Р = ур . +Р +Р +Р

z i—i gzt cez cmz ggz ’

где Р j, Pgzj — радиальная и тангенциальная составляющие сил при

микрорезании единичным зерном; Pcw, Раг — радиальная и

тангенциальная составляющие сил от контакта материала со связкой круга; Рст,, Рсш — радиальная и тангенциальная составляющие сил от

контакта материала со стружкой, заполняющей поры круга; Р, Р

— радиальная и тангенциальная составляющие сил резания от воздействия гидродинамических потоков в области контакта заготовки с кругом.

Уравнения (5.7) и (5.8) определяют силы резания на единицу длины условной режущей кромки абразивного зерна. Выделим в зоне контакта заготовки с кругом для момента времени т элементарный объем с глубиной А и, высотой Az и шириной, равной длине контакта Lk абразивного круга с обрабатываемой поверхностью по образующей. Число абразивных зерен ААЬ, вершины которых одновременно находятся в выделенном микрообъеме, определятся по плотности распределения /(и)

AAb = Lkngf (u)AuAz.

Введем понятие условной длины режущей кромки абразивных зерен выделенного микрообъема bv(hу). Если бы все точки площадок

износа вершин абразивных зерен контактировали с обрабатываемым материалом, то условная длина режущей кромки микрообъема определялась бы произведением ширины площадки износа на число зерен ААЬ. С учетом вероятности контакта

bz(hg) = b(l, g)PtAXb =b(hg)[l-P(M)]AXb.(5.16)

Величина суммарных сил, действующих на абразивные зерна, вершины которых расположены в выделенном микрообъеме, вычислится произведением сил, определяемых по уравнениям (5.7) и (5.8), на длину условной режущей кромки микрообъема

=Pg>,b(hg)[l-P(M)]Ltngf(u)bu&z;(5.17)

m^=Pglh(hg)=Pg! bihg)[l-P(M)]Lkngf(u)Au^. (5.18) При переходе от дискретной модели к непрерывной после

подстановки значений Р, Р, Р(М), f(u) уравнения (5.17) и (5.18) принимают вид

£(‘/b(z) ^25sin(3-or =- I j ( — ^ + 0,5b(z))i „ x

/7/w — —

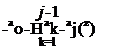xLknji1 lb(h) exp

Для определения сил резания по уравнениям, кроме законов распределения вершин зерен по глубине необходимо иметь и законы изменения величин площадок износа. В общем случае они устанавливаются на основании анализа работы единичного зерна в круге.

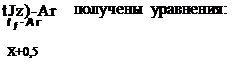При моделировании вершины зерна параболоидом, величины размерного износа зерна — степенной зависимость при

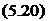x[0,96B{%;zm + 3,5)(tf — Ar)f? lllux В(x;2zm + 2,5)];

7 sin Pj 6

„ _ *WV£m«(‘/ — Mx40i5x, Va..

‘Vw — .. X

H;

где /^(x;z/7? + 3,5), B(%:zm + 2,5) — значения табулированной бета-

функции, z — показатель степени в уравнении /?ц.

Погрешность вычисления составляющих сил по уравнениям (5.19) и (5.20), вызванная принятыми приближениями, не превышает

10… 15%,

При значениях коэффициентов z=5 зависимость (5.19) принимает вид

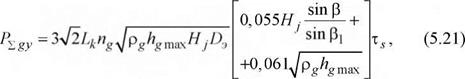
где Hj = Hu=tf-Ar.

Для процессов шлифования, когда износ круга происходит преимущественно за счет скалывания и вырывания зерен и на их вершинах не образуется значительных площадок износа, радиальная и тангенциальная силы могут быть рассчитаны на основе анализа напряженного состояния на поверхности контакта абразивного зерна — индентора с обрабатываемым материалом [119,142].

При движении индентора на поверхности полупространства возникают две зоны: зона проскальзывания и зона "прилипания". В зоне проскальзывания материал обтекает индентор, в зоне "прилипания" удаляется в виде стружки (зона схода стружки). Для каждой элементарной площадки контакта абразивного зерна с материалом могут быть выделены нормальные и касательные напряжения. Величина нормальных напряжений oN обычно принимается постоянной, направление касательных напряжений совпадает с направлением скольжения металла по поверхности абразивного зерна. Величины сил резания, действующих на абразивное зерно и инструмент в целом, вычисляются в этом случае как сумма составляющих от нормальных и касательных напряжений

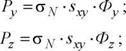(5.22)

(5.23)

где s — среднее суммарное сечение стружки; Фх, Ф. — безразмерные комплексы:

^ p(12pg +5tf — 2hc)yjhc(tf —hc)

Atf^Jlt/Pg

где hc — высота зоны проскальзывания.

Силы резания при работе круга в режиме самозатачивания зависят от характеристики инструмента, режима шлифования, физико­механических свойств обрабатываемого материала, коэффициента трения на площадке контакта зерна с материалом. В отличие от известных, уравнения (5.22) и (5.23) позволяют учесть влияние на силы пластичности обрабатываемого металла и объяснить причины отличия отношений радиальной и тангенциальной составляющих при обработке различных материалов. С увеличением пластичности уменьшается коэффициент стружкообразования, увеличивается зона проскальзывания и, как следствие, тангенциальная составляющая силы резания.

Если принять для случая шлифования нормализованной и закаленной стали коэффициент трения на площадке абразивного зерна с металлом равным 0,2, коэффициент стружкообразования соответственно — 0,35 и 0,9, то при глубине микрорезания

tj = 8…15.ШШ отношения Р2 / Ру будут равны:

для нормализованной стали — 0,52…0,64;

для закаленной стали — 0,30…0,40.

Отношение Pz /1, увеличивается с уменьшением коэффициента стружкообразования. Это подтверждается экспериментальными

данными работы [136], согласно которым Pz /1, для нормализованной

стали 45 составляет в среднем 0,63, для закаленной стали — 0,35, что соответствует расчетным данным.

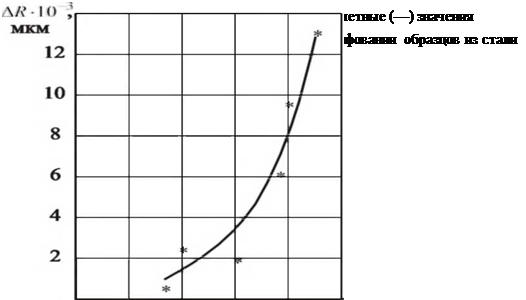
Для проверки предложенных зависимостей вычислены радиальная и касательная составляющие сил для различных режимов шлифования образцов из нормализованной стали 45 диаметром 60 мм кругами 1- 300x40x127 24А 25-Н С1 К. При расчетах принято на основании обработки экспериментальных данных работы [142] су N =18,9 ГПа, коэффициент стружкообразования Кс= 0,35, коэффициент трения электрокорунда по стали — 0,2. Выполненное сопоставление показало на хорошее соответствие расчетных и экспериментальных данных.

Полученные зависимости позволяют рассмотреть влияние износа и затупления режущих кромок на тепловые процессы в зоне контакта заготовки с кругом. По данным исследований работ [56, 57], температура на поверхности заготовки в точке выхода из зоны контакта вычисляется по зависимости

где Q — мощность теплового источника; — коэффициент

теплопроводности обрабатываемого материала; %и — коэффициент температуропроводности материала.

Мощность теплового источника пропорциональна

тангенциальной составляющей силы резания, скорости резания и обратно пропорциональна площади контакта инструмента с заготовкой. При работе круга в режиме затупления с увеличением времени возрастают площадки износа на вершинах зерен, повышаются силы резания, уравнения (5.7), (5.8), что приводит к увеличению температуры шлифования. Так, при шлифовании кругами 24А 25-Н СТЗ К с /„ =0,01 мм температура на обрабатываемой поверхности за

о

период стойкости инструмента может увеличиваться в 1,5…2 раза. При снижении прочности закрепления в связке круга затупившиеся зерна вырываются, что способствует снижению температуры. При работе круга в режиме самозатачивания влияние времени работы инструмента на температуру незначительно.

Таким образом, рассмотренная динамическая теоретико — вероятнастная модель износа абразивного инструмента позволяет:

1. Выполнить анализ закономерностей работы единичных абразивных зерен инструмента с момента их активации (с начала прохождения через зону контакта инструмента с заготовкой) до момента разрушения или вырывания из связки круга. Аналитически определены: глубина резания единичным зерном на каждом обороте круга; длина пути резания единичным зерном; износ единичных зерен; вероятность разрушения единичного абразивного зерна.

2. Установить взаимосвязь износа абразивного инструмента с износом и закономерностями работы единичных абразивных зерен, что открывает новые возможности совершенствования конструкций инструмента.

3. Предложены разностные и интегро-дифференциальные уравнения износа инструмента, установлены начальные и граничные условия для их решения. Более полно раскрыты закономерности влияния характеристики и режима обработки на закономерности работы инструмента.

4. Рассмотренные модели позволяют объяснить механизм изменения сил резания и температур за период стойкости инструмента. Они могут быть использованы для расчета стойкости инструмента и назначения его твердости из условия обеспечения заданного физико-механического состояния поверхностного слоя.