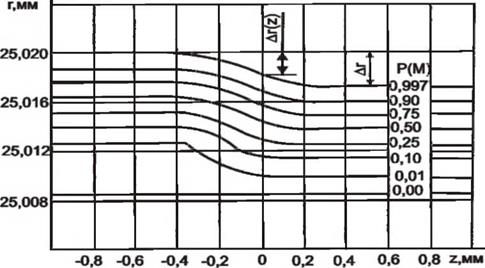
Полученные в разделах 4.5 и 4.6 зависимости позволяют рассмотреть методику аналитического расчета радиального съема материала по входным технологическим переменным процесса шлифования. Как отмечалось в разделе 3.3, граничная область материал — среда может быть задана уровнями равной вероятности удаления материала. При прохождении поверхности зоны контакта уровни смещаются к центру заготовки, рис. 4.20.
|
Рисунок 4.20 — Изменение радиус-векторов уровней равной вероятности |
Наблюдая за изменением положения уровня Р(М) = (3„;,
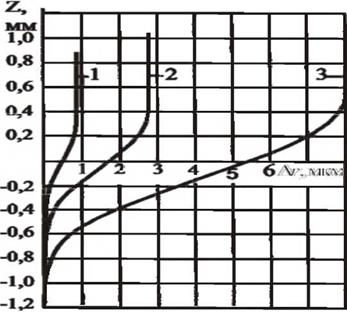
ограничивающего переходную область материал — среда со стороны среды, можно проследить за динамикой удаления припуска в зоне контакта заготовки с инструментом. Расстояние между радиус — векторами исходной поверхности и поверхности после контакта будет определять радиальный съем материала А г за касание, а положение линии с вероятностью Р(М) = (3„, в течение контакта — текущее значение радиального съема и форму кривой, ограничивающей зону контакта со стороны инструмента, рис.4.21.
|
Рисунок 4.21 — Влияние глубины микрорезания tj на радиальный съем материала при шлифовании заготовок из закаленной стали кругами 24А 25- НСМ2 4Б: 1- tf =0,005 мм; 2 — tf =0,01 мм; 3 — tf =0,02 мм |
Наиболее интенсивное уменьшение радиус-вектора заготовки наблюдается вблизи плоскости, проходящей через центр круга и центр заготовки, когда глубина микрорезания t(z) максимальна и через сечение проходит наибольшее количество режущих кромок инструмента. Уравнение линии, ограничивающей зону контакта заготовки с кругом со стороны инструмента (линия AnD"C рис. 4.1,
б), запишется, если придать в уравнении (4.39) вероятности удаления материала значение (3„,
Р т =1 — exP(-«o — а-а2-…- ctj_i — aj (у)).
Величина съема материала за j — й контакт поверхности с кругом числено равна смещению к центру заготовки уровня с принятой вероятностью удаления материала и вычисляется из уравнения (4.41), которое при у ■ =0 может быть записано
-1п(1 — Р, я) = Gj(t (j — A r-f +Так + %■
к=
 |
 |
 |
На основании полученного уравнения
 |
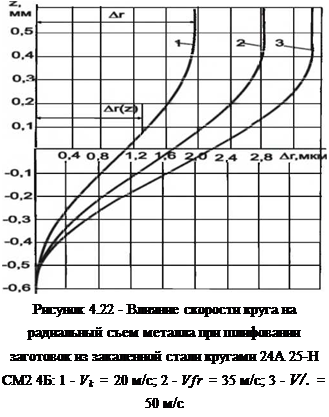Численное решение уравнения (4.44) выполнено на ЭВМ для условий шлифования стальных образцов кругами зернистостью 25. Результаты представлены на рис.4.22 .. .4.23.
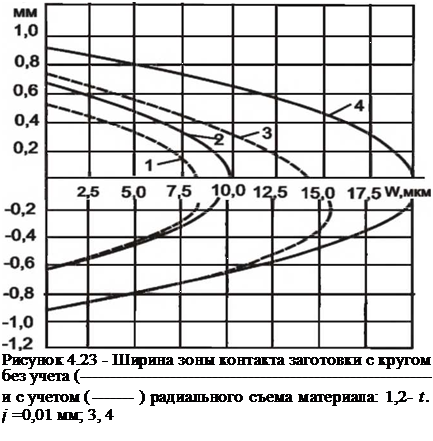
В отличие от процесса фрезерования, с которым часто сопоставляется процесс шлифования, линии контура заготовки носят плавный характер. В области точки А” (входа сечения в зону контакта, см. рис. 4.1) и в области точки С” (выхода сечения из зоны) они плавно переходят в окружности. Размеры и форма зоны, рис.4.23, несколько отличаются от известных в литературе [75, 160, 148]. Фактический размер зоны по координате z на 75…80% больше, чем принимаемый при запятообразных срезах и на 10… 15% меньше, чем принимаемый при сегментообразных срезах. Ширина зоны отличается от максимально возможной на величину текущего радиального съема материала (см. рис. 4.23).
z,
 |
— t. j = 0,02 мм
Радиальный съем материала определяется режимом шлифования, состоянием поверхности инструмента, размерами
заготовки и круга, состоянием обрабатываемой поверхности после предшествующего контакта. При установившемся процессе шлифования для вывода зависимости радиального съема от элементов режима шлифования в явном виде с учетом многопроходности процесса совместим начало координат с уровнем максимальных вершин профиля на (у-и)-м касании, где п — число касаний поверхности с кругом, необходимых для полного обновления микрорельефа
Р(М) = 1 — exp {-G Г (/у — уj_n )v + (tf-yj_„+ Arf +…+
 |
Произведем в уравнении (4.45) замену переменной tj на Н + Аг и переменной у на у’+Н. При Р(М) = Зда после преобразований получим
-1п(1-(3„,) = аГ(Лг-/)у +(2Ar-y’)v + … + («Ar-/)v], (4.46) где у’ — расстояние от нижней границы шероховатости поверхности после (j — п) — го контакта до рассматриваемого уровня.
Если 0 <, у’ < Аг, то весь слой, в котором распределена шероховатость, будет сошлифован при
(n + Y)Ar-y’ = tj. (4.47)
Уравнения (4.46) и (4.47) при выбранном значении вероятности (3„, позволяют рассчитать радиальный съем материала и толщину
граничной области материал — среда. Приближенное решение системы может быть найдено, если предположить, что п является величиной непрерывной. В этом случае через п касаний поверхность, ограничивающая шероховатость сверху, переместится на величину у = Н. После подстановки в уравнение (4.46) Аг из уравнения (4.47) при у’ =
^ 1 + 2V +… + гї’
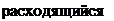Многочлен ——————
(h + 1)v
ряд. При х =1,5 и т =0,5 зависимость имеет вид почти прямой линии. Наибольшее отклонение от прямой имеет место при числе касаний, равном нулю и единице. При шлифовании л не может быть равно нулю, так как для удаления исходной шероховатости всегда необходим контакт обрабатываемой поверхности с кругом.
При достаточно широком изменении элементов режима резания число касаний л, которые нужны для полного удаления исходной шероховатости поверхности, меняется в пределах от 2 до 12. Наиболее значительно число касаний увеличивается с уменьшением глубины микрорезания tj. В исследуемом диапазоне рассматриваемый
 |
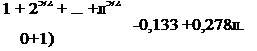многочлен при х =1,5, т= 0,5 может быть заменен зависимостью
В таблице 4.4 приводятся данные по соответствию многочлена линейной зависимости. Данные показывают, что при замене многочлена линейной зависимостью погрешность расчетов не превышает 1% на крайних точках.
|
Таблица 4.4 — Сопоставление значений многочлена и функции
|
После замены многочлена на линейную зависимость и решения уравнений (4.46), (4.47) и (4.1) относительно А г, tj и Н получим
Уравнения (4.48) и (4.49) являются приближенным решением системы уравнений (4.46) и (4.47). Они могут быть использованы, как для оценки и анализа самого процесса, так и для определения начальных значений Дг и п при решении системы на ЭВМ.
Сопоставление величин радиального съема металла, вычисленного по зависимости (4.48) и системе уравнений для случая шлифования образцов из закаленной стали кругами зернистостью 25 при диаметре заготовки 50 мм, диаметре круга 300 мм, приводится в табл. 4.5. Для большинства режимов шлифования отклонение значений радиального съема металла не превышает 1%. Только для
|
Таблица 4.5 — Расчетные значения радиального съема материала
|
для режимов 4 и режимов 4 и 9 они составляют 1,2 и 1,9 %. Таким образом, принятые приближения обеспечивают достаточно высокую точность расчетов и позволяют аналитически оценить влияние на радиальный съем материала и слой шероховатости поверхности элементов режима шлифования и характеристики абразивного инструмента. Радиальный съем и слой шероховатости поверхности зависят от фактической глубины микрорезания, скорости заготовки, размеров заготовки и круга, геометрии абразивного зерна, числа режущих кромок на поверхности круга.
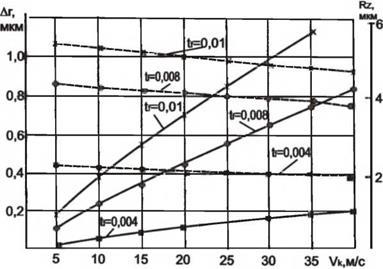
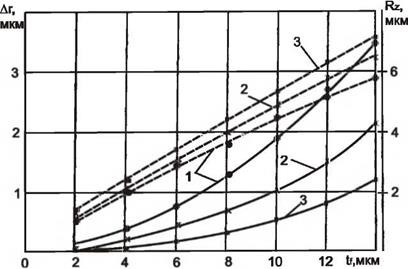
С увеличением глубины микрорезания радиальный съем материала и слой шероховатости поверхности увеличиваются для всех значений скорости круга и скорости заготовки, рис. 4.24 и 4.25.
|
Рисунок 4.24 — Влияние скорости круга на радиальный съем (———- ) и высоту неровностей профиля по десяти точкам (———— ) при шлифовании образцов из закаленной стали кругами 24А 25-Н СМ2 4Б |
В исследованном диапазоне слой шероховатости поверхности изменяется почти пропорционально t. j. Так, для кругов зернистостью
25 при увеличении tf в 2 раза, с 4 до 8 мкм, при Vu =0,5 м/с слой
шероховатости увеличивается в 1,85 раза, с 1,98 до 3,66 мкм. Радиальный съем материала с увеличением глубины микрорезания увеличивается более значительно, чем слой шероховатости поверхности. Так, при увеличении tj с 4 до 8 мкм радиальный съем
увеличивается в 3,5 раза, с 0,38 до 1,34 мкм. Такое влияние глубины микрорезания на радиальный съем объясняется тем, что при увеличении t у увеличивается не только толщина, но и длина
единичных срезов.
С увеличением скорости круга радиальный съем увеличивается, слой шероховатости поверхности уменьшается. С увеличением скорости заготовки при tj= const радиальный съем материала
уменьшается, слой шероховатости поверхности увеличивается, рис. 4.25.
|
Рисунок 4.25 — Влияние глубины tj и скорости заготовки на радиальный съем металла (—— ) и высоту неровностей профиля по десяти точкам (——- ) при шлифовании образцов из закаленной стали кругами 24А 25-Н СМ2 4Б со скоростью заготовки: 1 — 0,15 м/с; 2 — 0,25 м/с: 3 — 0,5 м/с |
С целью экспериментальной проверки полученных зависимостей были проведены опыты по шлифованию образцов из закаленной стали 9X2. Образцы диаметром 50 мм и длиной 250 мм шлифовали на станке ЗБ153 кругами 1-300x20x75 24А 25-Н СМ2 Б
при скорости круга 35 м/с, скорости заготовки 0,262 м/с. Для того чтобы каждая точка поверхности за один проход встречалась с кругом один раз, продольную подачу на оборот заготовки выбирали равной высоте круга.
По полученным экспериментальным значениям радиального съема металла за проход (одно касание поверхности заготовки с кругом) вычисляли максимальную глубину микрорезания и слой шероховатости поверхности. Величину слоя сравнивали с экспериментальными значениями, полученными по профилограммам шлифованной поверхности.
Пример. Рассчитать величину слоя шероховатости поверхности при шлифовании образцов из закаленной стали диаметром 50 мм кругами
|
Таблица 4.6 — Влияние поперечной подачи на радиальный съем металла и глубину микрорезания
|
Полученные зависимости радиального съема металла и слоя шероховатости поверхности от поперечной подачи аналогичны имеющимся в литературе. Если аппроксимировать их уравнениями
вида Н = CHS", то показатель степени при Sv будет равен 0,44, что
хорошо согласуется с экспериментальными данными других авторов.
Сравнение расчетных и экспериментальных данных указывает на их соответствие при всех значениях подач. Несколько отличен наклон расчетной кривой, наибольшее отклонение (17,5%) расчетных значений от экспериментальных наблюдается при поперечной подаче 1 мкм/ход. При увеличении поперечной подачи различия в расчетных и экспериментальных значениях шероховатости поверхности уменьшаются. В области поперечных подач 4-8 мкм/ход экспериментальные значения становятся больше теоретических. Незначительные различия экспериментальных и теоретических значений в области подач 1-2 мкм/ход могут быть объяснены тем, что при вычислениях число вершин на поверхности круга принято постоянным, в то время как оно по данным Opitz Н. [189] увеличивается с уменьшением интенсивности съема металла и поперечной подачи. Но и при сохранении числа абразивных зерен постоянным уравнения (4.49) и (4.50) достаточно хорошо моделируют реальный процесс шлифования.