Вычисление вероятности удаления материала в зоне контакта заготовки с кругом

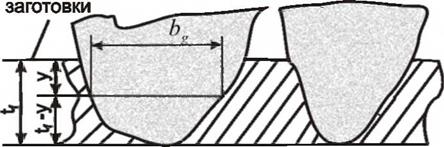
Необходимым условием полного физического моделирования процесса шлифования, по данным С. Н. Корчака [57], является учет одновременной обработки металла несколькими зернами в зоне контакта заготовки с кругом. Съем материала единичными абразивными зернами в зоне соответствует при формализованном описании изменению вероятности удаления материала. До входа в зону контакта заготовки с кругом обрабатываемая поверхность, как правило, имеет определенный микрорельеф. Он сформирован либо на предшествующих операциях, либо в самом процессе шлифования и может отличаться от микрорельефа, который обеспечивается после очередного контакта поверхности с кругом. Если поверхность получена в результате воздействия инструмента, не имеющего регулярной геометрии, то вероятность удаления материала с учетом наличия исходной шероховатости определяется по зависимости

Р(М) = 1 — е~а(уУа(У^ (4.19)

где а(у) — показатель, определяющий вероятность удаления материала на уровне у до входа поверхности в зону контакта заготовки с кругом; а{у, х) — показатель, определяющий изменение вероятности удаления материала на уровне у в зоне контакта.

Не выясняя физическую природу показателя а(у) и его связь с предысторией процесса формообразования, рассмотрим изменение вероятности удаления материала на фиксированном уровне у при одном контакте поверхности с инструментом. Съем материала при шлифовании производится дискретными порциями, но число единичных срезов, проходящих через сечение, достаточно велико (от нескольких сотен до нескольких тысяч на единицу длины сечения), что позволяет при расчете вероятности перейти от дискретной модели к непрерывной.

Расчет вероятности удаления материала для различных процессов обработки абразивными инструментами отражает особенности кинематики движений заготовки и инструмента. Наиболее простой схемой шлифования является обработка поверхности торцом круга за один или несколько проходов. Такая схема реализуется, например, при шлифовании торцом на станках карусельного типа, двухстороннем торцовом шлифовании и ряде других операций.

Рассмотрим последовательность и варианты расчета вероятности удаления материала на примере плоского шлифования с продольной подачей, рис. 4.9. Выделим элементарный участок, расположенный на расстоянии у от поверхности заготовки. При движении заготовки абразивные зерна начинают проходить через участок в момент времени t. Q и заканчивают в момент времени /]. За время контакта снимается слой материала А г, на поверхности остается слой

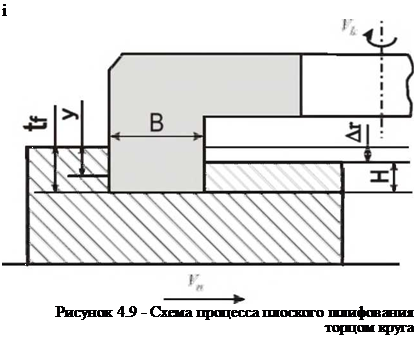шероховатости Н. Скорость резания при контакте участка с кругом изменяется в связи с изменением радиуса его контактирующей поверхности.

Напомним некоторые полученные ранее зависимости: Вероятность удаления материала вычисляется Р(М) = 1-е

Г~л —^А/[/>р] — Cl

вероятность неудаления материала — г(М) = е * =е, для

предварительно обработанной поверхности Р(М) = Р(М0)е~а^у, х размер профиля зерна на расстоянии h от вершины.

Вначале предположим, что все вершины абразивных зерен лежат на условной наружной поверхности инструмента и внедряются в обрабатываемый материал на одинаковую глубину, рис. 4.10. Подобная схема часто встречается в литературе и положена в основу теории шлифования материалов, предложенной Е. Н. Масловым [76]. Анализ схемы позволит дать оценку погрешности математических моделей, построенных при принятии такого допущения и разработать рекомендации по совершенствованию моделей с целью повышения их адекватности.

Поверхность

Рисунок 4.10- Схема к расчету вероятности удаления материала при расположении вершин зерен на одном уровне

Число абразивных зерен, проходящих через единичный участок поверхности при постоянстве скорости резания за время т, вычисляется

Я = ngVkx.

Если скорость резания изменяется, как это следует из рис. 4.9 для торцового шлифования, то следует вычислить элементарное приращение X за время dx

dX = ngVkdx.

Расстояние от вершины зерна до рассматриваемого уровня, рис. 4.10, определится как tf—y, ширина поверхности резания на

рассматриваемом уровне — bg = Cb(tj — у)т. На основании этого приращение показателя а вычислится

da = ngVkCh(tf — у)т dx. (4.20)

Скорость круга вычислим по частоте его вращения vk, продольной подаче Vu и максимальному радиусу круга Rmax

Vk=2Tzvk(Rmax-Vtlx). (4.21)

После подстановки полученного значения скорости в уравнение (4.20) получим относительно простую зависимость

/

а = 2л v kCbng (tf — yf (Rmax — Vux )dx .

о

После интегрирования определим

a=nvkCbng(tf — y)’"t(2Rmas — до­выполним численную оценку полученной зависимости для случая шлифования стальных заготовок кругами 25 зернистости при tj =20 мкм, tj—y = 1 мкм, /77 = 0,5, Vu=0,2 м/с, ширине 5=10 мм,

/=0,05 с, Q, = 2^2р^ , pg=2lMKM, ng=5,2 1/мм2, 5,^ = 125мм,

vA =44,6 Гц.

о = 3,14• 44,6• 2V2 • 21 • 10_6 ■5,2-Ю6(МО"6)0’5 -0,05(2-0,125- -0,2-0,05) = 117;

Р(М) = е-117 *0.

Таким образом, результаты численных расчетов показывают, что вероятность неудаления материала на рассматриваемом уровне у = 19 мкм равна нулю, что противоречит экспериментальным данным. Замеры относительной опорной длины профиля на этом уровне, проведенные по профилограммам обработанной поверхности, дают оценку значений Р(М) от 0,6 до 0, 7. Из этого следует, что принятое при расчетах допущение, что все абразивные зерна расположены на одном уровне и внедряются на одинаковую глубину, приводит к большим погрешностям. Математические модели при принятии этого допущения не адекватны реальным процессам шлифования.

Снимем указанное допущение и примем, что вершины абразивных зерен расположены не на одном уровне, что доказано многочисленными экспериментальными исследованиями.

Распределение режущих кромок по глубине рабочей поверхности инструмента изучено в работах [152, 159, 153, 160, 168]. При аналитическом описании кривых распределения Ж. Кассен принимает, что число режущих кромок на поверхности круга пропорционально квадрату расстояния внутрь круга [160]. Кривая плотности вероятности распределения режущих кромок моделируется им прямолинейной зависимостью /(и) = Сjii. Как отмечает автор,

моделирование кривой распределения прямолинейной зависимостью справедливо для участка круга, непосредственно лежащего вблизи поверхности. Ono Kojl [168] предлагает применять для
математического описания распределения вершин зерен по глубине степенные зависимости вида

где Су — коэффициент, вычисляемый из условия равенства единице площади, ограниченной кривой распределения,

где Ни — величина слоя рабочей поверхности круга по глубине, в пределах которого подсчитывается число абразивных зерен.

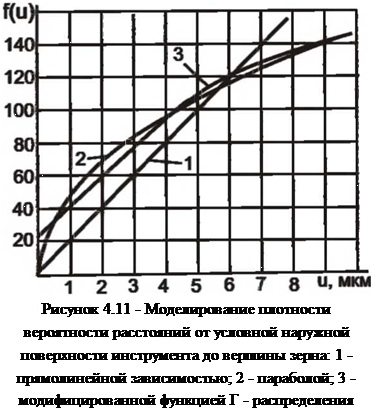Сопоставление значений плотности вероятности распределения для различных моделей, рис. 4.11, свидетельствует, что наиболее значительное отличие от динамического распределения имеет прямолинейная зависимость. Лучшее приближение обеспечивает степенная зависимость при % = 1,5.

Степенные зависимости в настоящее время широко применяются не только для математического описания распределения вершин зерен на рабочей поверхности шлифовальных кругов, но и для математического описания распределения зерен по высоте хонинговальных брусков.

Через единичный участок поверхности толщиной du, рис. 4.12, расположенный на расстоянии и от условной наружной поверхности инструмента за время dx пройдет dX вершин абразивных зерен.

dX = ngf (u)duVkdx.

Ширина профилей этих зерен на уровне у от поверхности заготовки будет равна bg = Cbh"’ = Cb{tj — у — и)т,

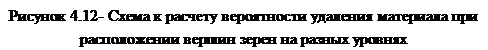
Поверхность заготовки

а приращение показателя а определится

После подстановки в уравнение (4.23) значения I) из уравнения (4.21) вычислим а

После интегрирования зависимости (4.24) получим а = + 2 _ (4 25) #м*Г(т+ Х+1)

где Г(%), Г(т +1), Г(т + % +1) — соответствующие гамма-функции.

Рассмотрим численный пример расчета вероятности неудаления материала по зависимости (4.25) при значениях переменных первого варианта и у =1,5, Н и = 20 мкм. Значения гамма-функции

Г(т +1) = Г(1,5) = 0,886; Г{т + % +1) = Д3) = 2.

3,14-1,5 -5,2 -106 -44,6-2-/2-21-1(Г6 -0,886-0,886 „

ц =————————————————————- (2 • 0,125 -0,05-

(20 -КГ6)1’5 -2

+0,2-0,052)(М0’6)2 =0,745; ДМ) = е-0’745 = 0,474; ДМ) = 0,526.

Полученное значение вероятность неудаления материала достаточно хорошо соответствует экспериментальным данным. Модели, учитывающие распределение вершин зерен по глубине инструмента более адекватны реальным процессам шлифования.

Для процесса круглого наружного шлифования рассмотрим изменение вероятности удаления материала на фиксированном уровне у при одном контакте заготовки с инструментом.

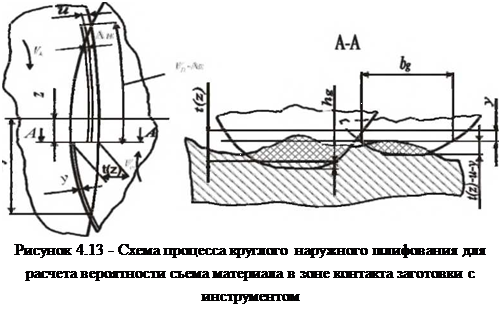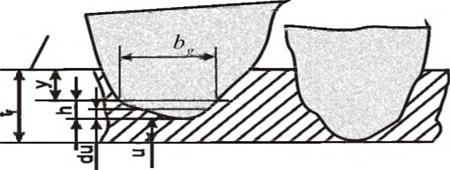
Для фиксированного положения сечения в зоне контакта, рис. 4.13, сечение А-А, материал заготовки будет удаляться только теми зернами, расстояние до вершин которых от условной наружной поверхности инструмента меньше t(z) — y. Выделим из них зерна с

координатой и, t(z) — у>и> 0, где и — расстояние от условной наружной поверхности до уровня в рабочем слое инструмента по направлению радиус-вектора. При прохождении через сечение их профиль пересекается уровнем у на расстоянии h = l(z)-у-и от вершины.

Ширина контура вершины, соответствующая данному уровню, при моделировании степенной зависимостью (2.10) вычисляется по уравнению:

Расчет вероятности удаления материала в любой области зоны контакта при известном исходном состоянии поверхности выполним при подстановке а(у, т) = а из уравнения (4.32) в уравнение (4.19). Для наглядности процедуры расчета приведем численный пример.

Пример. Рассчитать вероятность неудаления и удаления материала при шлифовании заготовок из закаленной стали диаметром 48 мм кругами 1-300x20x127 24А 25-Н СМ2 Б при скорости круга 35м/с, скорости заготовки 0,25 м/с, продольной подаче 33 мм/с, поперечной подаче 0,008 мм/ход. Из расчета баланса перемещений определяем, что для заданных условий обработки tj =0,01087 мм. На

основании данных исследований [13,21,76] принимаем: Кс= 0,9;

2 ТТ v>

р3 =0,021 мм; п3= 5,2 зерен/мм. Для рассмотренных условий Lv =0,53×10"’ м. Расчет выполним по уравнению (4.32) для уровня у =0,004 мм при z=-0,l мм:

37Cл/2-21 -10-6 -0,9-5,2-Ю6 -35,25-(10,87-10_6 — 4-Ю-6)2

8-0,25(10,87 -10-6)3’2

3(0,53-10“3)2 5(0,53-10“3)4 15

Показатель а() определен по профилограмме исходной шероховатости поверхности. Для уровня 0,004 мм он равен 0,546. Вероятность удаления материала вычислим по уравнению (4.19)

Р(М) = 1 — с-0’5464’23 = 0,83.

Вероятность неудаления материала соответственно определится (уравнение 4.19)

Р(М) = 1-ДМ) = 1-0,83 = 0,17.

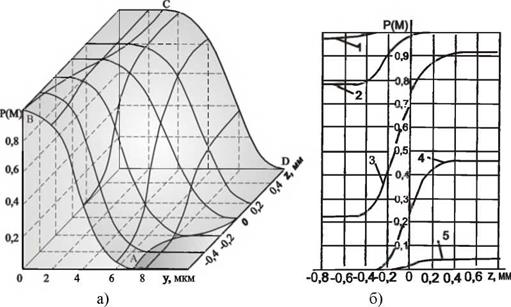
Для других уровней у рассматриваемого примера расчетные данные по вероятности удаления материала приведены на рисунке 4.14.

Рисунок 4.14 — Изменение вероятности съема материала в зоне контакта при шлифовании образцов из стали 9X2 кругами 1-300x20x127 24А 25- Н СМ2 Б при Vfc = 35 м/с, Sx = 2 м/мин, /у = 0,01087 мм: 1 — у=1 мкм; 2 — у =3 мкм; 3 — у =5 мкм; 4 — у =7 мкм; 5 — у =9 мкм

Линия АВ, рис. 4.14, а, характеризует соотношение удаленной и неудаленной части металла вследствие наличия на поверхности исходной шероховатости. Линия СД соответствует вероятности удаления металла после прохождения поверхности зоны контакта круга с деталью. Линии, расположенные в плоскостях, параллельных плоскости Р(М), Z и вынесенные на рисунок 4.14, б, отражают изменение вероятности в пределах дуги контакта на фиксированных уровнях.

Полученные данные показывают, что при прохождении поверхности зоны контакта круга с заготовкой вероятность удаления металла увеличивается в пределах фактической глубины резания на всех уровнях. Наиболее интенсивно вероятность повышается при
z = 0, что соответствует положению сечения вблизи основной плоскости. Это объясняется тем, что в этот момент времени глубина резания максимальна и в резании участвует наибольшее число абразивных зерен.

Предложенные зависимости позволяют проследить закономерность съема припуска в пределах дуги контакта шлифовального круга с заготовкой. Закономерность съема припуска на рисунке 4.14, а определяется линией ВС, имеющей уровень вероятности Р{М) = 0,9973. Радиальный съем металла при выходе поверхности из зоны контакта круга с деталью составляет для рассмотренного примера 3 мкм, что достаточно хорошо соответствует экспериментальным данным — Дг = 3,37 мкм.

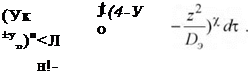Для характеристики процесса формообразования значительный интерес представляет также вычисление числа абразивных зерен, проходящих через элементарный участок поверхности. Приращение числа зерен в общем виде определяется по уравнению (4.27), которое после подстановки значений /(и) и переходе от дискретной модели к непрерывной принимает вид

После замены переменной т на — и интегрирования при

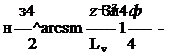X = 1,5, получена зависимость для расчета текущего значения числа режущих кромок, проходящих через сечение:

Число режущих кромок, которые проходят за время контакта сечения с кругом, определится из уравнения (4.35) при верхнем пределе интегрирования z = Lv:

Для процессов плоского, внутреннего шлифования зависимости для расчета показателя а(у,%) и вероятности удаления материала аналогичны зависимостям, полученным для круглого наружного шлифования. Для процесса плоского шлифования многочлен

.1—^— заменяется на, для процесса внутреннего шлифования — D + d

Dd

D-d ‘

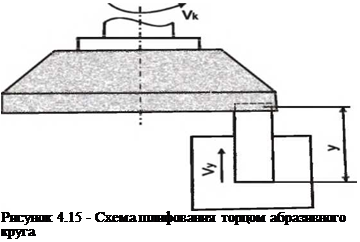Для процесса шлифования торцом круга с поперечной подачей, рис. 4.15, расчет вероятности съема материала выполняется в такой же последовательности, как и для круглого наружного шлифования. Особенностью этого вида шлифования является то, что обрабатываемая поверхность может контактировать с кругом непрерывно. При этом для установившегося процесса шлифования размер заготовки изменяется пропорционально времени обработки. Для участка поверхности, расположенного на расстоянии у от базовой плоскости заготовки, материал начинает удаляться в момент времени t. Q, когда вершины наиболее выступающих абразивных зерен начинают проходить рассматриваемый уровень. Материал полностью удаляется после выхода уровня из зоны контакта заготовки с кругом.

Элементарное приращение показателя а для рассматриваемого процесса, как и для процесса круглого наружного шлифования, определится произведением размера сечения профиля зерна на их число в элементарном объеме круга толщиной А и, шириной 1 м и длиной Ук Дт. Аппроксимируя функцию распределения /(«)

степенной зависимостью и профиля вершины зерна параболой, получим

t гГУ

a(t) = ngVkKc J J bgf (it)ditch.

0

После интегрирования помиї зависимость принимает вид

где К, — скорость движения режущего профиля круга в материале заготовки в направлении подачи; /0 — время начала удаления

материала на рассматриваемом уровне абразивными зернами, которые находятся на условной наружной поверхности инструмента.

Как и при круглом наружном шлифовании, при шлифовании торцом круга вероятность удаления материала увеличивается с увеличением скорости круга, подачи и числа абразивных зерен на рабочей поверхности инструмента. Значительное влияние на вероятность оказывают также параметры формы режущих кромок и их распределения по глубине инструмента.

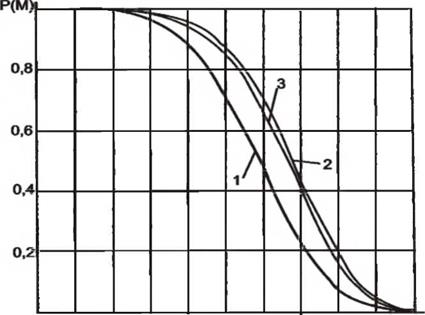
Несмотря на известную степень приближения, зависимости (4.19), (4.33) и (4.38) достаточно хорошо моделируют процессы удаления материала в зоне контакта заготовки с кругом. Если принять гамма-распределение за наиболее точную модель распределения зерен по глубине круга, то максимальное отклонение расчетных значений вероятности удаления материала наблюдается при моделировании f(n) пропорциональной зависимостью, рис. 4.16.

1 2 34 56 789 У, мм Рисунок 4.16- Кривые вероятности удаления материала при моделировании плотности вероятностей расстояний от вершин абразивных зерен до условной наружной поверхности инструмента: 1 — прямолинейной зависимостью; 2 — параболой; 3 — модифицированной функцией Г — распределения

При моделировании f(u) степенной зависимостью при т = 0,5 значения вероятностей удаления материала отличаются не более чем на 4 — 5%.

Анализ уравнения (4.19) позволяет проследить влияние на съем материала наложения единичных срезов друг на друга. Если бы единичные срезы не накладывались, то для полного удаления материала на заданном уровне было бы достаточно, чтобы сумма длин поперечных размеров вершин зерен равнялась длине сечения, например 1 мм. Однако расчеты по формуле (4.19) показывают, что вероятность удаления при а = 1 равна 0,63, т. е. только 63% материала будет удалено, а 37% останется на поверхности в виде микронеровностей. Такая закономерность наблюдается вследствие того, что единичные срезы накладываются друг на друга, часть абразивных зерен вообще попадает в единичные риски, не производя работы резания. У значительной части вершин зерен контакт с материалом будет неполным, он распространяется не на всю ширину абразивного зерна. С увеличением числа режущих кромок, проходящих через сечение, число единичных срезов, накладывающихся друг на друга, увеличивается. Так, при вероятности удаления материала Р{М) = 0,9 показатель степени при е равен 2,3, т. е. сумма поперечных размеров зерен, проходящих через сечение, в 2,3 раза больше длины рассматриваемого участка. При вероятности съема Р(М)=0,9975 показатель а равен 6,0. Следовательно, только 1/8 часть суммарного сечения зерен находится в контакте с материалом.

Рассмотренные особенности изменения вероятности удаления материала при контакте обрабатываемой поверхности с абразишым инструментом и предложенные аналитические зависимости справедливы для широкого диапазона режимов шлифования, характеристик кругов и ряда других технологических факторов.

Такие элементы режима, как скорость круга и скорость заготовки, непосредственно входят в уравнение для расчета вероятности удаления материала, поперечная подача, хотя и не представлена непосредственно в уравнении, но она определяет максимальную глубину микрорезания tj.

При увеличении скорости круга показатель а увеличивается, увеличивается и вероятность удаления материала.

С увеличением скорости круга за время контакта поверхности заготовки с кругом через сечение проходит большое количество абразивных зерен. Число зерен увеличивается пропорционально скорости, пропорционально скорости круга увеличивается и показатель а. Влияние скорости заготовки на вероятность удаления и показатель а противоположно влиянию скорости круга. С увеличением скорости заготовки уменьшается время контакта сечения с кругом, уменьшается число режущих кромок, проходящих через сечение. При сохранении соотношения скорости круга и скорости заготовки постоянными характер зависимостей, величина показателя а и вероятности удаления материала после контакта остаются неизменными.

Влияние характеристики инструмента и состояния его рабочей поверхности на вероятность удаления материала отражено радиусом закругления при вершине зерна, числом режущих кромок на рабочей поверхности инструмента и их распределением по глубине. С увеличением числа зерен и радиусов закругления вероятность удаления материала увеличивается.