Максимальная глубина микрорезания для процесса круглого наружного шлифования определяется геометрически по величинам межцентрового расстояния и размерам радиус-векторов инструмента и заготовки. В соответствии с размерной цепью, представленной в левой нижней части рис. 4.1, б, имеем
А = R — tf +г.
На основании этого
tf=R + r-A. (4.6)
Составляющие правой части уравнения (4.6) необходимо определить с учетом упругих и температурных деформаций элементов технологической системы. Обозначим радиус-вектор поверхности круга в цилиндрических координатах R(у, х, т), радиус-вектор
поверхности заготовки — г{ср, х,т) и представим уравнение (4.6) в виде
tу = R( у, х, т) + г{ ср, х, т) + ARq — ARV + А г — A rv — А, (4.7)
где AR ARv, Ar Arv — соответственно температурные и упругие деформации заготовки и круга.
Радиус-вектор круга определяется по уравнению (2.27), величина межцентрового расстояния — по размеру статической настройки Аст, величине упругих AAv и температурных AAq
деформаций приспособления, станка и величине отклонений расстояния от среднего значения вследствие наличия вибраций в технологической системе
^ — А^ст А ААу + AAq cos(xraov/ +|/ ov;),
і
где Avi, movi,\)ovi — амплитуда, циклическая частота и фаза /-й гармоники изменения межцентрового расстояния при вибрациях.
Анализ уравнения (4.7) показывает, что в общем случае максимальная глубина микрорезания в евклидовом и временном пространствах является случайным многомерным процессом. Если известны параметры заготовки, инструмента, температурные и упругие деформации, то могут быть рассчитаны математическое ожидание, корреляционная функция и дисперсия глубины микрорезания. Необходимо также учесть, что при шлифовании режим резания за период обработки одной поверхности изменяется по циклу. Наиболее часто используются циклы, включающие этапы: врезания, чернового шлифования, чистового шлифования и выхаживания. С изменением режима изменяется и максимальная глубина микрорезания. Изменения наблюдаются и при переходе с одного этапа цикла на другой. Шлифованию свойственны переходные процессы функционирования системы. Без учета фактических координат подсистем и элементов, а также изменения глубины резания, как правило, бывает невозможным прогнозирование выходных переменных операции.
Рассмотрим изменение глубины резания в процессе обработки заготовки при отсутствии вибраций. Для этого запишем уравнение (4.6) для двух последовательных контактов участка обрабатываемой поверхности с кругом
![]() tfj~Rj+rj~Aj
tfj~Rj+rj~Aj
lfj-1 =Rj-+rH~Aj-l
Выразим в системе (4.8) параметры j — го контакта через параметры j-І — го контакта и соответствующие приращения
O‘ у-1+ А0 j = Rj-1- А/0/ + 0-1 “ АОн — Aj-+
*, (4.У)
tfj~l =Rj-+rj- ~Aj~ 1
где Atу j — изменение глубины микрорезания при j-м контакте;
ARvj — изменение радиуса круга вследствие наличия износа, упругих и
температурных деформаций за время от совмещения радиус-вектора рассматриваемого участка поверхности заготовки с основной плоскостью при j-1-ом и j-ом контактах; Д/у/_| — радиальный съем
материала при j-1-ом контакте в сумме с приращениями упругих и температурных деформаций за время между контактами; AAvj —
соответствующее изменение межцентрового расстояния.
Вычитанием из первого уравнения системы (4.9) второго после несложных преобразований получим
= Atf j + ARvy + Aav,_j. (4.10)
Изменение расстояния между центрами вращения круга и заготовки вычислим для процесса круглого наружного шлифования по методу врезания по поперечной подаче, упругим и температурным деформациям технологической системы
Му = Ms] — Му] — ^(4.11)
где AAS ■, tsAVj, tsAqj — соответственно, изменения межцентрового
расстояния вследствие наличия подачи, упругих и температурных деформаций за время от совмещения радиус-вектора рассматриваемого участка поверхности заготовки с основной плоскостью при j-1-м и j-м контактах.
Зависимости вида (4.11) могут быть записаны и для изменений радиус-векторов круга и заготовки. В связи с этим общая зависимость баланса перемещений в технологической системе запишется
Ms j = А// j + + Д/>-1+ £ АУф + £ АУф» (4-12)
к- к-
где ARj и Д/у_і — радиальный износ инструмента и радиальный съем
П т
материала в ранее принятые интервалы времени; ^ AyVJк и ^ ^Уф ~
к= к=
суммы приращений упругих и температурных деформаций элементов технологической системы. Знак плюс присваивается, если приращение уменьшает глубину резания и знак минус — если увеличивает.
Для установившихся процессов обработки уравнение
(4.12)может быть решено при применении метода итераций.
Анализ зависимости (4.12) показывает, что поперечная подача на j-ом обороте (проходе) расходуется на приращение глубины микрорезания, компенсацию радиального съема материала предшествующего оборота, износ круга, приращения упругих и температурных деформаций. Радиальный износ инструмента и радиальный съем материала зависят от глубины микрорезания, приращения упругих и температурных деформаций. Уравнение (4.12), в отличие от известных, имеет в правой части приращение глубины микрорезания, которое в ряде случаев может быть больше других слагаемых. Так, для современных круглошлифовальных станков при диаметре обрабатываемой заготовки до 100 мм податливость системы шпиндель шлифовальной бабки — шпиндель передней бабки составляет от 0,02 до 0,03 мкм/Н. При шлифовании кругами высотой 40 мм, зернистостью 25 радиальная составляющая силы резания равна 100… 150 Н. Следовательно, упругие отжатия в системе лежат в пределах от 2 до 4,5 мкм [58], а глубина микрорезания меняется от 4 до 18 мкм [54,55,127] и по своей абсолютной величине значительно превышает упругие деформации.
С целью пояснения структуры уравнения (4.12) рассмотрим элементарный пример расчета баланса перемещений в технологической системе для процесса круглого наружного врезного шлифования с поперечной подачей ДАу =5 мкм на оборот заготовки и
частотой ее вращения v„ =2 Гц. Время одного оборота заготовки равно 0,5 с. Для расчетов воспользуемся очень грубыми приближениями: ARj =0,1/у j; Ат/Ч = 0,2/ ^. , ^; AAVJ = 0,2A/y/ .
Приращения упругих деформаций круга и заготовки, а также температурных деформаций элементов системы не учитываем. Начальное состояние системы /у0 = 0. Подставим принятые значения
параметров в уравнение (4.12)
AASJ- = А/ j j +0,11j y_] +0,2/ j j_j + 0,2А/у j.
Для первого контакта поверхности с инструментом имеем 5= A/yj +0,1-0+0,2-0+0,2-A/yj; A/yj =5/1,2=4,17; t^ =0+4,17=4,17 мкм.
Для второго и третьего контактов вычислим:
5= А//2 +0,1 -4,17+0,2-4,17+0,2- Мf2; Atf2 =3,75/1,2=3,12;
//2=4,17+3,12=7,29;
5= Atp +0,1 -7,29+0,2-7,29+0,2- Atf3; Atp =2,81/1,2=2,34;
tf3=7,29+2,34=9,63.
Результаты дальнейших расчетов сведены в табл. 4.2.
|
Таблица 4.2 — Изменения глубины резания, износа круга, съема материала, упругих деформаций при круглом наружном шлифовании
|
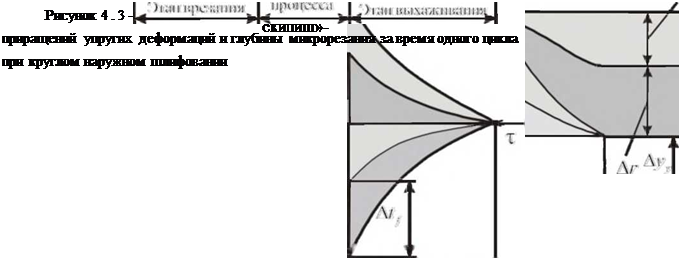
Схема изменений приращений AR, At j, Аг и
Ayv = AAV + ARV + Arv за период обработки одной заготовки приведена
на рис.4.3. При ее построении приращения температурных деформаций приняты равными нулю и исключен чистовой этап цикла. Более точный расчет баланса перемещений выполняется после выражения составляющих уравнения (4.12) через технологические факторы.
При шлифовании без предварительного натяга на этапе врезания в начальный момент времени почти вся поперечная подача идет на приращения упругих деформаций в системе и глубины микрорезания. С увеличением t. j увеличиваются радиальный съем
материала и износ круга, поэтому для дальнейшей части процесса приращения деформаций и глубины уменьшаются, а на этапе установившегося процесса они стремятся к нулю. Величина поперечной подачи на этом этапе почти полностью расходуется на радиальный съем материала и износ круга.
На этапе выхаживания приращения упругих деформаций и глубины отрицательны и асимптотически стремятся к нулю при увеличении т. Уменьшение глубины приводит к снижению радиального съема и износа, которые при увеличении т также стремятся к нулю.
Для шлифования с продольной подачей расчет баланса перемещений выполняется аналогично. Размерный анализ процесса для двух последовательных проходов (см. рис. 4.2) приводит к двум основным уравнениям
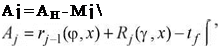
 |
(4.13)
где /у_|((р, л’) и Rj(y, х) — радиус-векторы заготовки и круга с учетом
температурных и упругих деформаций.
Уравнение (4.12) записано для дискретных процессов обработки заготовок абразивными инструментами, при выполнении которых
анализируемый участок поверхности вступает в контакт с абразивным инструментом периодически. Для непрерывных процессов обработки приращения необходимо заменить на соответствующие производные.
Таким образом, выполненное описание показывает, что для прогнозирования пространственного положения элементов технологической системы необходимо иметь сведения о параметрах качества заготовки, исходного профиля инструмента и аналитические модели, определяющие связь с технологическими факторами глубины микрорезания, радиального съема материала, износа круга, сил резания, упругих и температурных деформаций.
