Для большинства процессов обрабатываемая поверхность не может быть представлена как простое геометрическое копирование формообразующего поля, так как взаимодействие режущих кромок и материала сопровождается комплексом сложных физических и химических явлений. В то же время трудно назвать процессы, для которых бы наблюдалось абсолютное несовпадение обработанной поверхности и поля. Многочисленные экспериментальные данные показывают, что, как правило, существует тесная корреляционная, а в ряде случаев и функциональная связь между ними как по макро-, так и микрогеометрическим параметрам.
Описание макрогеометрических параметров поверхности выполняется обычно в координатах обрабатываемой заготовки. При описании базового участка за начало отсчета целесообразно принять поверхность впадин (в сечении — линию впадин), координаты которой определяют по координатам условной границы поля, величине упругих и температурных деформаций материала заготовки.
Описание геометрических параметров обработанной поверхности, как и формообразующего поля, можно выполнить двумя методами: а) заданием формы, геометрических размеров, законов распределения единичных рисок, кратеров, сколов; б) заданием поверхности функционалами случайного поля.
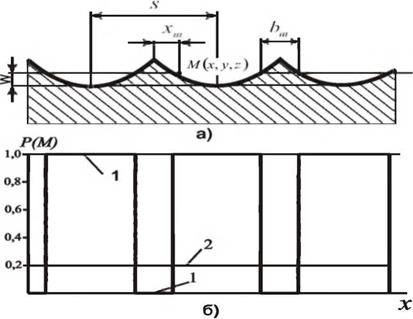
Для анализа процесса формообразования рассмотрим в граничной области материал — среда произвольную точку M{x, y,z), рис. 3.4, а. Для каждой такой точки можно говорить о двух событиях: о событии, заключающемся в том, что материал в этой точке будет удален, и о событии противоположном, заключающемся в том, что материал в точке останется неудаленным. Каждое событие случайно и имеет определенную вероятность. Назовем вероятность первого события вероятностью удаления материала, второго — вероятностью неудаления материала, введя соответствующие обозначения Р(М) и
Р(М). Сумма вероятностей равна единице, а значения вероятностей в общем случае могут зависеть от положения точки в граничной области по всем трем координатам. Например, если начало координат для поверхности с регулярным микропрофилем совместить с вершиной одного из выступов шероховатости, то при постоянстве формы единичных рисок, их глубины и равенстве расстояний между рисками 5 вероятность удаления материала на уровне W будет функционально зависеть от координаты А" (см. рис. 3.4, а).
|
Рисунок 3.4 — Схема поверхности а) к анализу граничной области материал — среда и вероятность удаления материала б) при жестком (линия 1) и нежестком (линия 2) закреплении профиля относительно начала координат |
Если расстояние точки до ближайшей вершины микропрофиля
I I ^ Ът
— 2 ’ т0 веРоятность удаления материала равна нулю, так как
точка лежит в пределах выступа шероховатости поверхности, и вероятность удаления материала равна единице, если точка лежит за пределами указанного интервала. График зависимости вероятности удаления материала представляется в виде кусочной функции со значениями нуль и единица (рис. 3.4, б, линия 1).
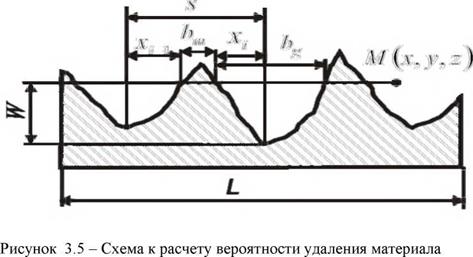
Если профиль обработанной поверхности стационарен и относительно начала координат по оси X жестко не закреплен, то вероятность неудаления материала на уровне W, рис. 3.5, определяется по пределу отношений суммы длин отрезков Ьт, заполненных материалом, к длине сечения L, стремящейся к бесконечности,
Р{М) = Нш ——- . (3.11)
L—»со Е
|
|
Поскольку сумма выступов, заполненных материалом, при Е-> да стремится к 1ХМ[Ьт ], уравнение (3.11) может быть записано в виде
Р(М) = 1-Р(М) = 1-Ш[Ьт], (3.12)
где X — математическое ожидание числа выступов на единицу длины сечения; МЬт] — математическое ожидание ширины выступа
шероховатости поверхности на заданном уровне W.
Для расчета вероятности неудаления материала по зависимости (3.12) необходимо определить X и МЬт]. Математическое ожидание числа выступов шероховатости с учетом выступов с размерами Ьт =0 равно математическому ожиданию числа впадин поверхностей резания и определяется конструкцией инструмента и кинематикой процесса.
Для точения
X = l/sQ,
где sQ — продольная подача резца на один оборот заготовки; Для торцового фрезерования
X = 1 / sz,
где sz — подача на один зуб фрезы.
Для шлифования X равно среднему числу зерен, проходящих через единицу сечения.
Размер і — го выступа в нормальном сечении поверхности определяется расстоянием между рисками s и размерами y_j, у от впадин рисок до точек профиля, ограничивающих выступ шероховатости, рис.3.5:
Для обтачивания и фрезерования, для случая, когда поверхности резания имеют одинаковую геометрию и располагаются на одном уровне, сумма расстояний y_j и у равна ширине сечения
поверхности резания bgна рассматриваемом уровне. Уравнение (3.13)
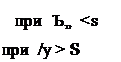 |
||
может быть записано в виде:
Для токарной обработки все переменные, входящие в уравнение (3.14), можно считать детерминированными величинами и поэтому в пределах слоя шероховатости поверхности при bg < s
Р(М) = —bm = 1 — — (ctgip + ctgcpj), (3.15)
so >
где cp и cpi — соответственно главный и вспомогательный углы резца в плане.
Для процесса торцового фрезерования расстояние между двумя соседними поверхностями резания является величиной случайной в связи с наличием биения зубьев фрезы. По данным выполненных исследований расстояние от центра вращения фрезы до вершин режущих элементов распределено по нормальному закону с параметрами среднего радиуса Гф и среднеквадратическим отклонением а.
Из теории вероятностей известно, что если случайная величина Y является функцией ф(х) случайной величины X, то математическое ожидание Y вычисляется по зависимости
СО
М[7] = j g>(x)f(x)dx, (3.16)
—со
где /(х) — плотность вероятностей распределения случайной величины X.
Для фрезерования зависимость (3.16) для расчета
математического ожидания размера выступа шероховатости
принимает вид
СО л
W[/>J= f (.v,-/>,)—t—e 2“2 dsz, (3.17)
h. <W 2k
&
где Jz — среднее расстояние между поверхностями резания.
При выводе зависимости (3.17) второе условие системы (3.14) учтено в пределах интегрирования.
Зависимости (3.15) и (3.17) получены при условии постоянства расстояний jc,_| и х;. В действительности же они являются величинами случайными. Для токарной обработки отклонения от среднего вызваны вибрациями, возникающими в технологической системе, для фрезерования — колебаниями и биением зубьев в вертикальном направлении, при шлифовании, кроме перечисленного, — непостоянством формы режущих кромок и различием их расстояний от условной наружной поверхности инструмента по глубине. Если все параметры, входящие в систему (3.13), являются случайными, то математическое ожидание Ьт вычислится
СО СО со
МК = \ j О — У — )/VY;_, >х. (.V, у_,, у )dsdxi_ldxi, (3.18)
О 0 .Yj-.j+.Yj’
где fsx ] v. (s, Xi_,Xj) — совместная плотность распределения
случайных величин s, Xj_i, Xj (см. рис. 3.5).
Уравнение (3.18) справедливо как для случайных, так и для регулярных профилей, так как любая детерминированная величина может рассматриваться как случайная при одном её возможном значении. Например, при точении в условиях отсутствия вибраций, упругих и пластических деформаций в пределах слоя шероховатости всегда s > х, + у_1.
Случайные величины, входящие в уравнение (3.18), чаще всего бывают независимыми. Так, например, размер поверхности резания на заданном уровне никак не зависит от расстояний между траекториями движения вершин абразивных зерен, а размеры і-го абразивного зерна — от размеров /-1-го зерна. При независимости случайных величин вычисление математического ожидания значительно упрощается. Уравнение (3.18) в этом случае запишется
СО СО со
м К = і J J о — У — У-i )Л(*)Д_, (У-і )./л — (у )dsdxi_ldxi. (3.19)
О 0 хг_!+хг
При почленном разложении уравнения (3.19) его можно интегрировать сначала по х; и у_|, а затем по s. Интегралы
ОС 00
fx і (xi )dxi и j fx ;_i (у_і)й6с;_і равны единице, а интегралы
СО X
xifxi(xi)dxi и jУ-і/х i-(xi-)dXi- ~ соответствующим
математическим ожиданиям М|х; | и М[х;_] | случайных величин х; и Xj_i. С учетом изложенного, уравнение (3.19) принимает вид
M[hm]= ] (s-M[xi]-M[xj_l])fs(s)ds. (3.20)
A/fxJ+A/fx^j]
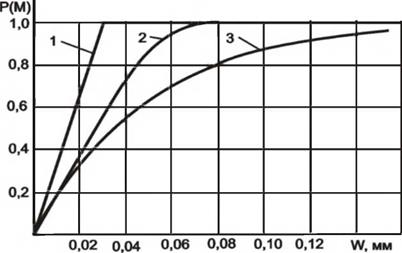
Из (3.20) следует, что на эффективность и качество процессов формообразования существенное влияние оказывают и параметры распределения расстояний между вершинами элементов поля в направлении оси абсцисс. На рис. 3.6 приводятся данные по вероятности удаления материала для трех вариантов: 1) расстояние между профилями сечений элементов поля постоянно (точение, строгание; 2) расстояния распределены по закону Гаусса (фрезерование); 3) расстояния распределены по показательному закону. При расчетах принято, что все вершины элементов формообразующего поля, имеющие форму конуса с углом 90Р, лежат на одном уровне со средним значением расстояний между впадинами Г =0,1 мм. Математическое ожидание числа поверхностей резания X =10 1/мм, дисперсия для закона нормального распределения а =0,03 мм. Приведенные данные подтверждают ранее высказанную гипотезу о значительном влиянии закона распределения и его параметров на вероятность удаления материала.
С переходом от постоянства расстояний между поверхностями резания к их распределению по нормальному закону вероятность удаления материала, например для уровня W= 0,03 мм, снижается в 1,9 раза, а при переходе к показательному закону — соответственно в 2,2 раза.
|
Рисунок 3.6 — Изменение вероятности удаления материала в переходной зоне материал — среда |
При наличии на поверхности отклонений формы величина вероятности удаления материала будет определяться не только
выбором координаты Y, но и координат X и Z. В то же время для каждого из возможных сочетаний X и Z может быть вычислена ордината граничной области, рис. 3.7, для которой вероятность удаления материала принимает заданное значение (Зд/ .
|
Рисунок 3.7 — Уровни равной вероятности удаления материала в переходном слое материал — среда |
Совокупность таких точек образует в пространстве поверхность, а в сечении — линию равной вероятности удаления материала. Изменяя уровень вероятности, получим семейство поверхностей (линий) равной вероятности (см. рис. 3.7), а задавшись максимальным и минимальным уровнями, например Р(М) = р/шш = 0,00135 и Р(М) = П1ах = 0,99885, — две поверхности, ограничивающие
область материал — среда сверху и снизу.
По изменению положения уровней равной вероятности можно судить о пространственных отклонениях обрабатываемой поверхности и об изменении величины слоя, в котором распределена шероховатость.
По сравнению с относительной опорной длиной профиля, которая вычисляется по профилограмме только для конкретной реализации микропрофиля, вероятность удаления и вероятность неудаления материала отражают динамику процесса формирования поверхности. О вероятности удаления материала и её изменении можно говорить для любой точки пространства, в котором задана обрабатываемая поверхность. Относительная опорная длина профиля на базовой длине L непосредственно определяется по вероятности неудаления материала
1р=Цр(М)сЫ (3.21)
L Ї)
и численно равна ей, если Р(М) не зависит от х.
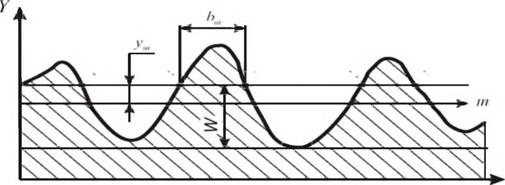
Функционал вероятности удаления материала относится к фунционалам, моделирующим обрабатываемую поверхность как случайное поле. Для поверхностей без жесткого закрепления профиля относительно начала координат он совпадает с функцией плотности распределения ординаты профиля детали Fw(W), рис. 3.8.
|
Рисунок 3.8- Схема к вычислению функции распределения ординат профиля обработанной поверхности |
В действительности функция распределения Fw(W) вычисляется:
Fw(W) = P(W <w).
где w — фиксированное значение случайной величины W.
Так как вероятность P(W < w) любого произвольного профиля поверхности равна вероятности попадания точки в интервалы отрезков АВ, СД, … и т. д., для которых W <w, то
L~Ybmi
P(W < w) = lim— j—— = P(M).
L—> со P
При полном геометрическом копировании на детали профиля
воспроизводящего ПОЛЯ
P(M) = Fw(W). (3.22)
Таким образом, при формировании поверхности в условиях преобладания одного из процессов вероятность удаления материала и функция плотности распределения ординат профиля определяются по параметрам воспроизводящего поля.