Рабочая поверхность инструмента может рассматриваться для процессов второй группы как совокупность отдельных базовых участков, а для процессов первой группы — как совокупность отдельных режущих кромок. При анализе процесса формообразования наиболее удобным является определение координат отдельных участков и режущих кромок инструмента относительно баз станка. Так, например, при фрезеровании можно говорить о биении режущих кромок относительно оси вращения шпинделя станка и относительно плоскости, перпендикулярной оси вращения. Для ряда процессов анализ формы инструмента относительно его базовых поверхностей не содержателен, так как рабочая поверхность формируется
непосредственно на станке, например, при шлифовании за счет правки круга.
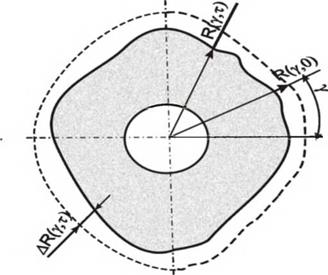
Рабочая поверхность инструмента, в зависимости от его вида, может задаваться в прямоугольных, цилиндрических и сферических координатах. Общие принципы её описания аналогичны принципам описания поверхностей деталей машин и приборов [55, 130, 125]. Отличительной особенностью является необходимость учета динамики изменения размеров и формы инструмента вследствие износа. Для вращающихся инструментов в сечениях плоскостями, перпендикулярными оси, профили рабочей поверхности представляются замкнутыми кривыми, рис. 2.12, радиус-вектор которых уменьшается с увеличением времени работы инструмента
R( У, x,t) = R(y ,x,0)-AR(y, x,t). (2.27)
в
|
Рисунок 2.12 — Текущий профиль вращающегося инструмента |
Значения, как исходного радиус-вектора R(y, x,0), так и величины износа AR(y, x,t), могут иметь как закономерные, так и случайные отклонения от своих средних значений. Изменение радиус — вектора в пространстве переменных у, х,х в общей постановке является случайным многомерным процессом. Для лезвийных инструментов угол у изменяется дискретно, случайный процесс вырождается в случайную последовательность.
Для фиксированного значения х исходный полярный радиус — вектор может содержать в спектре отклонений от своего среднего закономерные и случайные составляющие. Выделяя из уравнения (2.27) гармоники закономерных составляющих, запишем случайную функцию исходного профиля инструмента:
R( у, х,0) = Rq (х) + Aj (х) cos(/y +\i j (х)) +
Р (2.28)
+ X (l JRk sm wkJ + WRk cos wkJ I
k=
где Rq(x) — радиус средней окружности на расстоянии х от базовой
плоскости при т = 0 является величиной случайной, зависящей от погрешностей статической настройки станка при правке инструмента или погрешностей его изготовления; Aj(x) и ц/Дх) — амплитуда и фаза / — й гармоники; I! Rk и WRk — некоррелированные случайные величины с математическими ожиданиями, равными нулю, и дисперсиями, одинаковыми для каждой пары величин с одним и тем же индексом к.
Величина износа инструмента для фиксированного угла у зависит от условий контакта этого участка с обрабатываемой поверхностью и корреляционно связана с величиной исходного радиус-вектора, колебаниями припуска, твердости материала, частотой и амплитудой вибраций в технологической системе. Совокупность этих процессов приводит к появлению как закономерных, так и случайных отклонений в величине износа. При износе могут протекать процессы, способствующие выравниванию, сглаживанию рабочей поверхности, и процессы, способствующие увеличению закономерных и случайных отклонений. Для любого участка рабочей поверхности инструмента радиальный износ определяется скоростью износа SR{у ,х, т)
ЛЛ(у, х,/) =/5д(у, х,т)Л.
о
![]()
![]()
Математическое ожидание и дисперсия радиального износа для момента времени t вычисляются по математическому ожиданию и корреляционной функции скорости износа на основании свойств линейных операторов
В уравнение (2.33) входят одна гармоника закономерных составляющих исходного профиля и одна гармоника закономерных составляющих износа инструмента. В общем случае их может быть несколько. Последовательность анализа при этом сохраняется. Случайные компоненты / — й и / — й гармоник оставлены под знаком суммы, их анализ выполняется по аналогии с анализом других случайных отклонений.
Математическое ожидание случайной функции (2.33) вычисляется как сумма математических ожиданий отдельных слагаемых. Первое слагаемое является величиной случайной, распределенной по закону Гаусса, M[Rq(x)] = mR(x), математическое
ожидание второго слагаемого определяется по уравнению (2.29), математическое ожидание третьего и четвертого слагаемых равны нулю, математическое ожидание пятого слагаемого также равно нулю, поскольку случайные величины U и W центрированы. Таким образом
t
M[R{y, x,t) = mR{x)-ms{x, x)dx, (2.34)
о
где ms (х, т) — математическое ожидание скорости износа
инструмента.
Для вычисления корреляционной функции разобьем правую часть уравнения (2.33) на несколько независимых комплексов. Первый комплекс включает первое и второе слагаемые и определяет средний радиус-вектор в момент времени t. За период стойкости инструмента он, как правило, изменяется незначительно и не может существенно повлиять на процесс формирования отклонений профиля рабочей поверхности инструмента.
Для первого комплекса
Второй комплекс включает третье и четвертое слагаемые. Их корреляционная функция вычисляется как математическое ожидание произведения центрированных величин от аргумента Yj и у2
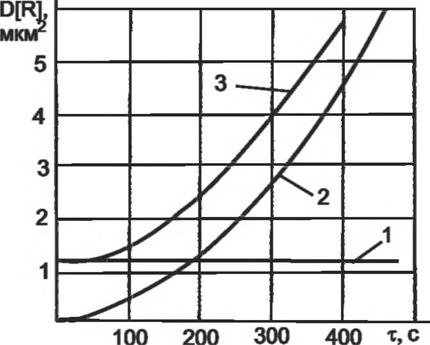
Дисперсия первого комплекса случайной функции (2.33) увеличивается при всех возможных комбинациях скорости износа инструмента, уравнение (2.42), рис. 2.13.
|
Рисунок 2.13 — Изменение дисперсии первого комплекса случайной функции профиля инструмента: 1 — дисперсия радиуса средней окружности исходного профиля; 2 — дисперсия радиального износа радиуса средней окружности; 3 — дисперсия радиуса средней окружности текущего профиля. |
Дисперсия второго комплекса периодической части процесса может, как увеличиваться, так и уменьшаться, рис. 2.14. Увеличение дисперсии наблюдается при сдвиге фаз исходных отклонений профиля
3 ж
и износа на величину —к >а^ > — , причем оно наибольшее при а,() = л . При сдвиге фаз на величину aV), = 0 в начальный момент
времени наблюдается уменьшение дисперсии, в момент времени т дисперсия второго комплекса становится равной нулю, а затем начинает увеличиваться. Дисперсия третьего комплекса случайной функции может, как увеличиваться, так и уменьшаться в зависимости
от величины коэффициента корреляции между случайными величинами
Профиль рабочей поверхности инструмента в продольном направлении может быть представлен как совокупность радиус — векторов в параллельных плоскостях при одинаковом угле у. При этом в каждом сечении радиус-вектор определяется по уравнению (2.33). С изменением расстояния от торца инструмента до сечения могут изменяться практически все переменные, определяющие радиус-вектор исходной поверхности и величину износа. При введении соответствующих зависимостей в уравнение (2.33) будет определена макрогеометрия рабочей поверхности инструмента. Для абразивных поверхностей, вследствие стационарности [110,111,105],
можно принять, что случайная составляющая исходного профиля и функции износа, фазы гармонической части отклонений профиля и износа не зависят от х.
При этих условиях в уравнении (2.33) с изменением координат х будет изменяться только первый комплекс (первое и второе слагаемые). Для случая, когда отклонения размеров среднего значения радиус-вектора и износа аддитивны и независимы
__ t__________ t
Rq (х, t) = Rq (0) + Фя (x) -jSR (0,T )dx — (x, T )dx,
о 0
где Ro{x, t) — усредненный по у радиус-вектор для времени t; Rq(0),Sr(0,t) — средний по у радиус-вектор рабочей поверхности инструмента и средняя скорость его износа при х = 0; ф^(х),ф^(х, т) — функции отклонений радиус-вектора и скорости износа от их средних значений.
Частные решения зависимости (2.41) приведены в работе [95]. Экспериментальную оценку предложенной модели выполнили при шлифовании образцов из стали ШХ15, HRC=50…55, размерами dxL = 50×150 мм кругами 1-400x40x127 24А 25-Н СМ2 6К на станке 3E153. Образцы шлифовали при скорости круга 33,5 м/с, скорости детали 1 м/с, продольной подаче 0,013 м/с. Профиль абразивного инструмента регистрировали специальной тензометрической установкой [95]. Запись профиля круга проводили при скорости его вращения 0,04 м/с на осциллографе модели К-22 непосредственно после правки круга алмазно-металлическим карандашом типа С с продольной подачей 3,3-10"’ м/с и после 10, 20 и 30 минут его работы на вышеприведенном режиме. Повторность опытов была принята равной пяти. Контактный наконечник тензометрической установки был изготовлен из твердого сплава с радиусом сферы 25 мм. Круглограммы круга табулировали и обрабатывали на ЭВМ. По методу наименьших квадратов определили коэффициенты йго, Хі, х2,…,Хзо и У,У2,—>Узотридцати первых частот ряда
R(у, т) = а0 +х} siny +ух cosy + … + x30sin30y + у30 cos30y, с последующим представлением результатов в виде случайной функции
i?(Y, x) = y40+y41sin(y +(/ J) + ^2 sin(2y +і|/2) + — + ^зо sin(30y +i|/30). (2.43) Математические ожидания и дисперсии амплитуд первых 22 гармоник уравнения (2.43) приведены в табл. 2.3. Погрешность определения амплитуд вычислена обработкой девяти независимых круглограмм. Она равна ±0,4 мкм.
|
Таблица 2.3 — Амплитуды и среднеквадратичные отклонения точек профиля рабочей поверхности шлифовального круга
|
С увеличением времени работы инструмента наиболее значительно увеличиваются амплитуды гармоник к = 2 и £ = 17. ..25. Распределение амплитуд гармоники к = 2 отклоняются от принятого ранее закона Рэлея, что показывает на возможность выделения случайной и закономерной составляющих, для т = 1800 с А=2 ~~ мкм.
Дисперсия отклонений в профиле инструмента для частот к >2 закономерно увеличивается примерно пропорционально квадрату времени работы инструмента, что подтверждает результаты аналитического анализа (см. рис. 2.14).Увеличение дисперсии профиля обусловливает заметное снижение точности формы обрабатываемой поверхности, для рассматриваемого примера с 1,5 до 5 мкм.
Полученные результаты позволяют сделать заключение о качественном соответствии предложенной модели реальному процессу. Анализ зависимости (2.42) и рис. 2.14 показывает на возможность активно влиять на процессы волнообразования на рабочей поверхности инструмента. Снижение высоты волнистости может быть достигнуто за счет периодического изменения частоты собственных колебаний системы «заготовка — центры». В этом случае волны, образовавшиеся на круге при периоде колебаний Тс, будут устраняться при обработке с увеличенным периодом ТС+АТС. Это происходит вследствие того, что заготовка наносит удары не по впадинам волн, а по вершинам и постепенно разрушает их. В результате имеет место явление, аналогичное «самоперерезанию» волн на обрабатываемой поверхности. Величина АТс, необходимая
для расчета периода измененных колебаний, определяется из анализа условия обеспечения минимальной дисперсии профиля и должна лежать в пределах четверти периода колебаний, то есть
О < АТГ < ^ с 4
В комплексе с функционалами базового участка зависимости изменения радиус-вектора представляют собой математическую модель рабочей поверхности инструмента. Модель является исходной при анализе параметров формообразующего поля и обработанной поверхности.