Распределение формообразующих элементов может рассматриваться на базовом участке рабочей поверхности и у инструмента в целом. Для процессов первой группы анализ распределения режущих кромок может проводиться только в пределах всего инструмента. Для процессов второй группы необходимо иметь функцию распределения элементов по трем координатам, две из которых X и Z направлены по касательным к рабочей поверхности, а третья — вглубь инструмента от его условной наружной поверхности.
f%xДгДи(*.*>“) = Р&х < ХЛ2 < 2 Ли < и где греческими буквами обозначены случайные величины: — расстояние от вершины элемента до условной наружной поверхности инструмента [1]; £,v,^r — расстояния от вершины элемента до начала координат по осям X и Z.
Для большинства процессов второй группы формообразующие элементы по осям X и Z распределены равномерно
ftx£z(x->z) = 7 у’
а плотность распределения расстояний до условной наружной поверхности инструмента предполагается известной и не зависящей от плотности распределения расстояний по координатам X и Z. По данным работы [134], для абразивно-алмазных инструментов закон распределения режущих кромок по глубине близок к нормальному.
На основании этого
Уравнение (2.15) не дает исчерпывающей информации о статистических характеристиках рабочей поверхности инструмента,
так как не содержит данных по распределению расстояний между элементами.
Если соседние вершины элементов располагаются независимо друг от друга, то расстояния между ними распределены по показательному закону. Для целого ряда процессов координаты вершины произвольно выбранного элемента зависят от координат других близлежащих вершин. Так, например, при электроэрозионной обработке наиболее вероятно возникновение разряда в области одного из выступов шероховатости поверхности. В результате расстояния между кратерами распределены по законам, отличным от показательного.
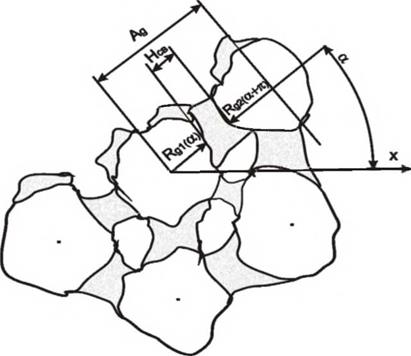
Плотности вероятностей расстояний между соседними элементами для многих процессов могут быть установлены аналитически. Так для абразивных поверхностей, рис. 2.8, расстояния между двумя центрами зерен Av = R }+R 2+HCfl распределены по
нормальному закону, если законы распределения радиусов R ^,R 2 и
размера мостиков связки Нсв нормальные.
|
Рисунок 2.8 — Схема к вычислению расстояний между формообразующими элементами рабочей поверхности инструмента |
Расстояния между вершинами зерен по осям в декартовых координатах определяются по углу а : Д = A cosa ; А = Ag sina.
Для фиксированного значения Ag = р условная плотность вероятностей fAgxi/’p) проекций расстояний при 2л >а >0 имеет вид:
а совместная плотность распределения случайных величин А и Ag определится произведением законов Гаусса и арксинуса:
Уравнение (2.17) справедливо для произвольной пары соседних формообразующих элементов. На рабочей поверхности инструмента вокруг рассматриваемого могут одновременно находиться т элементов. Расстояния между двумя любыми парами элементов можно считать независимыми. Вероятность события, заключающегося в том, что расстояние Ат от рассматриваемого до ближайшего соседнего
элемента окажется меньше некоторого заданного значения р, определится на основании закона о совмещении независимых событий
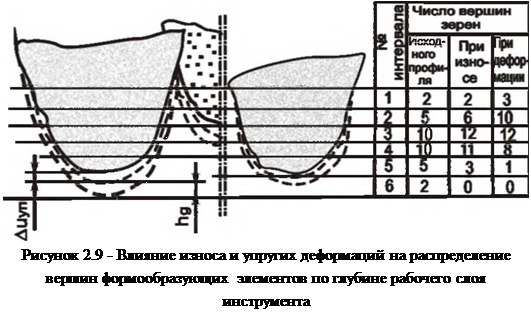
Для целого ряда процессов за период стойкости инструмента распределение формообразующих элементов не остается постоянным из-за износа и упругих деформаций, рис. 2.9.
 |
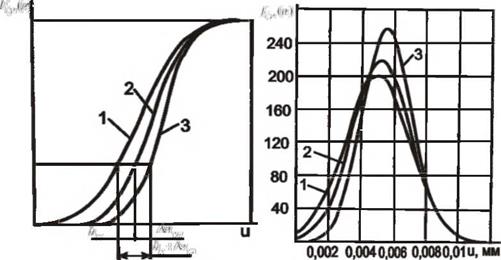
Так, для абразивных поверхностей интегральная кривая плотности Flu(u), рис. 2.10, а, и кривая плотности вероятностей, рис.
2.10, б, смещаются по глубине инструмента на величину износа h ^ и упругих деформаций. На основании этого
где индексами £и с„ т обозначены случайные расстояния от вершины
зерна до условной наружной поверхности инструмента для исходного и текущего профилей. Методика определения величины упругих деформаций рассматривается в работе [146].
Если величины износа и упругих деформаций пропорциональны глубине микрорезания, а исходное распределение нормально, то динамическое распределение также подчиняется закону нормального распределения.
|
а) б) Рисунок 2.10- Изменение распределения формообразующих элементов по глубине рабочего слоя инструмента: а) 1 — без учета упругих деформаций и износа круга, 2-е учетом износа, 3-е учетом износа и деформаций; б) 1 — т =0, 2-х =10 с, 3 — т =30 с |
Если величина износа не пропорциональна глубине, то динамическое распределение будет отличаться от нормального.
Например, при liv = Ch (Н-и)"х, рис. 2.10, б, наблюдается не только
смещение центра группирования исходного распределения, но и изменение формы кривых.