1.2. Форма режущих кромок рабочей поверхности инструмента
Описание базового участка рабочей поверхности абразивного инструмента предусматривает определение геометрических размеров, числа, распределения формообразующих элементов. Форма элементов зависит от их природы и вида. Для процессов обработки лезвийным инструментом она задается в виде неслучайных параметров. Для процессов второй группы элементы не имеют регулярной геометрии, их форма может быть смоделирована случайными функциями. Например, радиус-вектор точек контура абразивного зерна Rg(ср) по
данным А. В. Королева [54] является случайной функцией угла ср, рис. 2.1, а,
р
Rg(q>,0) = rg + X (хк sincoAxp + ук coscoAxp), (2.1)
к=2
где rg — радиус средней окружности профиля, определяемый как среднее значение функции 2? (ср,0); хк ук — случайные
некоррелированные амплитуды, соответствующие к — й гармонике и имеющие равные дисперсии; соА. — произвольно выбранная частота.
Уравнение (2.1) является результатом разложения случайной функции в ряд Фурье и приемлемо для описания формы практически любых единичных элементов рабочей поверхности инструмента.
При записи уравнения (2.1) в виде
р
Rg(q>,0) = rg + YJ Л sm(fap +МУ),
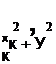 |
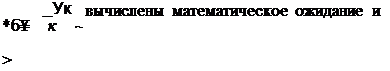 |
|
к=2
корреляционная функция радиус-вектора точек контура абразивного зерна
2
где rg0 и о,. — математическое ожидание и дисперсия средней
 |
окружности контура зерна; Ао/. и <з~)к — математическое ожидание и дисперсия амплитуды синусоид.
Уравнения (2.1) и (2.2) описывают статический контур (профиль) режущих кромок. Для целого ряда процессов форма кромок не остается постоянной, а существенно изменяется за период стойкости инструмента. Для процессов обработки деталей лезвийным и абразивным инструментами изменение формы кромок определяется их износом (см. рис. 2.1, б). Для единичного абразивного зерна текущий полярный радиус R„(ср, т) меньше его значения в статике на
о
величину износа hg{ср, х) за время т
![]() Rg (ф, т) = Rg (ф, 0) — hg (ф, т).
Rg (ф, т) = Rg (ф, 0) — hg (ф, т).
Элементарное приращение величины износа в направлении полярного радиуса может быть принято пропорциональным относительному износу hn и длине пути резания dLp(ф, т):
dhg{ср, х) = h0dLp{ф, т) = hQ(Vk ±Vu)Pk{cp, x )dx, (2.4)
где Vk и Vu — скорости круга и изделия (заготовки); /). (ср, х) — вероятность контакта точки профиля с материалом.
При токарной обработке сплошных поверхностей Рк = 1, Vk = 0, из уравнения (2.4) получаем известную в резании зависимость:
h = hQVuх.
При обработке деталей абразивными инструментами /^(ср, х) всегда бывает равно или меньше единицы, так как на поверхности имеются риски от исходной шероховатости или от ранее прошедших зерен. В общем случае вероятность контакта определяется как соотношение суммы отрезков, отсекаемых в материале на данном уровне, к базовой длине / —> оо и по величине совпадает с математическим ожиданием относительной опорной длины профиля. При микрорезании поверхности с регулярным профилем в ввде треугольных рисок, (см. рис. 2.1, а), вероятность контакта точки контура зерна вычисляется из соотношения
а дифференциальное уравнение (2.4) для точек профиля, находящихся в зоне микронеровностей, принимает вид
![]()
![]() K(VK±vu)
K(VK±vu)
где Я — величина слоя шероховатости поверхности; uR — расстояние от нижней границы слоя до центра зерна.
функция зависит не только от разности значений углов ф] и ср2, но и
от их абсолютных величин. При х = 0 математическое ожидание и корреляционная функция радиус-вектора Rg(ср, т) при вычислении по
зависимостям (2.6), (2.7) равны математическому ожиданию и корреляционной функции радиус-вектора точек исходного профиля зерна. Таким образом, по сравнению с известной, предложенная математическая модель является более общей. Она отражает кинетику изменения профиля формообразующего элемента за период стойкости инструмента.
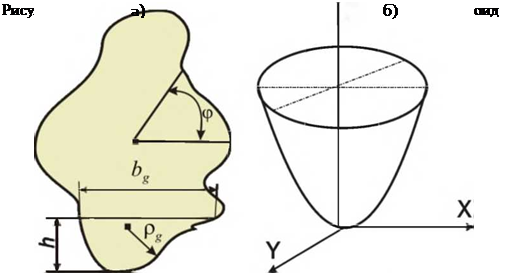 |
Другим возможным вариантом моделирования элемента рабочей поверхности инструмента является описание только той его части, которая непосредственно определяет процесс формообразования. При анализе операций обработки заготовок абразивными инструментами предполагают, что вершина зерна, выступающая над уровнем связки, может иметь форму конуса, конуса с закругленной вершиной, конуса с усеченной вершиной, шара [75, 131]. Более совершенной моделью вершины зерна является модель в виде параболоида вращения, рис. 2.2.
Уравнение параболоида при совмещении начала координат с пиковой точкой профиля записывается
г = -—у~, при у=0 na2=2pg x = ^2pgz,
где а — параметр параболоида; ре — радиус округления при вершине зерна.
Всесторонний анализ существующих моделей режущих элементов абразивных зерен, выполненный Л. В. Худобиным [141], показал, что модель в виде параболы является по сравнению с другими более предпочтительной и с высокой степенью точности соответствует экспериментальным геометрическим параметрам абразивных зерен. Если обозначить расстояние от вершины зерна до рассматриваемого уровня за h, то ширина профиля вершины bg на
этом уровне, рис 2.2, а, определится
bs = 2 у. (2.9)
Учитывая многообразие форм абразивных, алмазных, эльборовых зерен, уравнение (2.9) записывают в более общем виде
bg=Cbhm, (2.10)
в котором коэффициент Сь и показатель степени m определяют экспериментально.
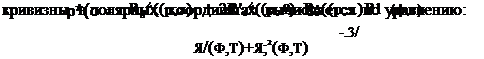 |
|
Вершина абразивного зерна может рассматриваться в общем его профиле как один из выбросов случайного поля со значениями Rg{ср) > р [121]. Для любой точки профиля абразивного зерна радиус
Радиус кривизны на участках выбросов может значительно отличаться от значения радиуса средней окружности. Аналитическое определение радиуса кривизны приводит к изучению главных кривизн к| и к2 профиля в точках локальных максимумов, превышающих
некоторый уровень. Для гауссовой однородной и изотропной случайной поверхности они вычисляются в работах [143]. На практике же, часто бывает значительно проще непосредственно изучить геометрические параметры вершин формообразующих элементов. По данным Д. В. Ваксера [21], З. И. Кремня [62] и других исследователей [47, 70], радиус при вершине зерна зависит от материала абразивного зерна, способа изготовления, зернистости, режима правки инструмента. Использование второго подхода при моделировании элементов рабочей поверхности инструмента в ряде случаев является более предпочтительным, так как по геометрии вершин накоплено больше практических данных, чем по геометрии зерен в целом.
При совмещении полюса полярных координат с центром кривизны вершины зерна для углов окрестности фр = 0 радиус-вектор
исходного профиля равен р а его текущее значение ДДфр, т)
определяется по зависимости (2.3), которая принимает вид:
Текущий радиус округления зависит от его исходного значения, условий контакта абразивного зерна с обрабатываемым материалом, режима резания и времени работы инструмента. С увеличением т
закономерно увеличивается р (т), на вершине зерна появляется
радиусная площадка износа, наблюдается затупление абразивного зерна.
Экспериментальная проверка закономерностей износа вершин формообразующих элементов выполнена при микрорезании образцов из стали У8 размерами d х L =71×235 мм зернами из карбида кремния зеленого и твердого сплава Т15К10. Исходную поверхность образцов подготавливали обтачиванием с продольной подачей 0,31 мм/об остро заточенным резцом с углом при вершине 75°. Величина слоя шероховатости исходной поверхности образца составляла 0,2 мм. Опыты проводили при частоте вращения детали 20,83 Гц, продольной подаче 0,21 мм/об, глубине микрорезания 0,16 мм. Профиль единичных зерен зарисовывали на инструментальном микроскопе при 50-ти кратном увеличении. Типичная картина изменения профиля вершин зерен карбида кремния зеленого после одного, двух, …, пяти проходов представлена на рис.2.1, б кривыми 2, 3, 4, 5 и 6 соответственно. В таблице 2.1 приведено сопоставление расчетных и экспериментальных значений радиуса округления вершины зерна по проходам для зерен из твердого сплава.
|
Таблица 2.1 — Изменение радиуса закругления вершин зерен
|
Отмечается закономерное увеличение радиуса вершины за счет износа. За один проход он возрастает в 1,2… 1,5 раза. Аналогичное изменение профиля вершин зерен наблюдается и в абразивном инструменте [135]. Притупление зерна закономерно увеличивается вплоть до его разрушения или вырывания из связки круга.
Рассмотренные особенности изменения профиля справедливы и для других формообразующих элементов. Аналогичная закономерность наблюдалась в изменении профиля вершин алмазов правящих инструментов.
